INDUCTION MUTUELLE:
lois de FARADAY et de LENZ
II Loi de Faraday: étude qualitative
III Lois de Faraday et de Lenz: étude quantitative
I Objectifs
|
 |
II Loi de Faraday: étude qualitative
A. Montage et acquisition
1. Montage
 |
 |
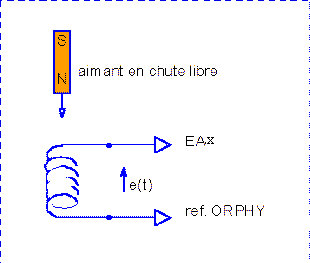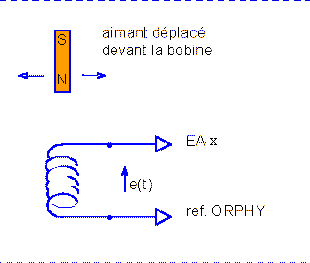
 | Principe: un inducteur (source de champ magnétique: par exemple un aimant permanent) est déplacé par rapport à un induit (bobine en circuit ouvert de 2*250 spires) |
| Les deux extrémités de la bobine sont reliées à l'entrée analogique (de plus faible calibre pour GTS) |
| L'inducteur est déplacé par rapport à la bobine dans différentes directions |
| Abscisse: | Voies actives: |
Enregistrement: |
Déclenchement (synchro): |
|||||
Temps |
EA: |
Variable: |
Signe: |
Cal: |
Unité: |
Nombre points: |
Durée: |
Manuel (Clavier ou clic sur bouton) |
t |
EA x |
e |
± |
50 |
mV |
100 |
5 s |
|
* avec ORPHY-PORTABLE 2 brancher capsule ±100 mV.
Charger l'acquisition pré réglée:
3. Protocole d'acquisition
Déclencher le balayage temporel, et commencer simultanément à déplacer l'aimant avec quelques mouvements de va-et-vient (parallèlement à la bobine, ou bien dans sa direction)B. Transfert vers Regressi
Ä t, et e
Dans la fenêtre 'Graphiques' (menu Fenêtre/graphe Variables),
cliquer-D pour choisir 'Coordonnées' dans le menu contextuel, ou cliquer-G sur l'icône
correspondante 
; vérifier que l'on a:
 | t en abscisses |
| e en ordonnées (à gauche). |
On a ainsi la représentation graphique de e = f(t). On peut déjà visualiser ses variations au cours du temps.
C. Étude qualitative de e(t)
Charger le fichier Regressi
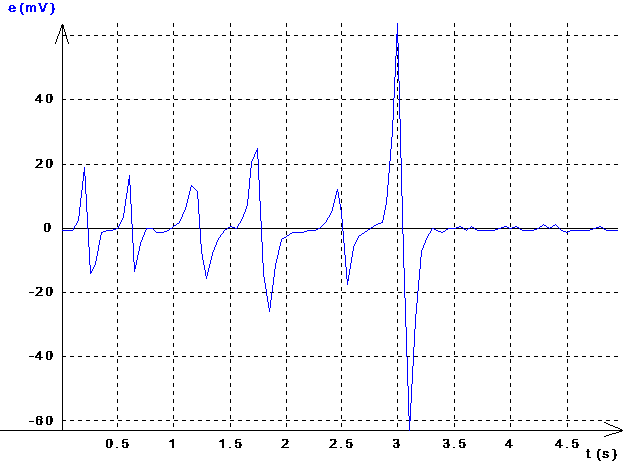
Quelques remarques s'imposent d'emblée:
| Il y une f.é.m. aussi longtemps que l'aimant est en mouvement, c'est à dire tant qu'il y a une variation de flux |
| Cette f.é.m. peut être positive ou négative |
| Sa valeur absolue peut varier dans des proportions importantes |
Le paragraphe suivant va chercher à vérifier la relation entre les variations de la f.é.m. et ses causes.
III Lois de Faraday et de Lenz: étude quantitativeA.
Montage et principe
|
 |
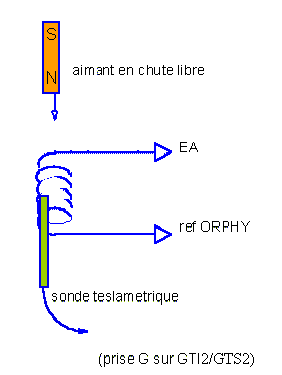B. Le capteur teslamétrique: nouveau capteur M12P302 pour prise DB15
(NB: pour l'ancien capteur à prise DIN 6 broches, voir paragraphe suivant)
|
SONDE TESLAMÉTRIQUE (réf M10416) |
 |
Les capteurs de cette nouvelle série pour prises DB15 (prises G, H, etc.) sont des capteurs à reconnaissance automatique: BRANCHEZ ET CA MARCHE!
|
Dès que le capteur est branché, le logiciel d'acquisition actualise l'affichage des voies actives pour le faire apparaître.
|
(1) BRANCHER:
|
|
(2) ETALONNER: CLIQUER sur la zone d'affichage du capteur pour accéder au bouton d'étalonnage:
|
 |
 |
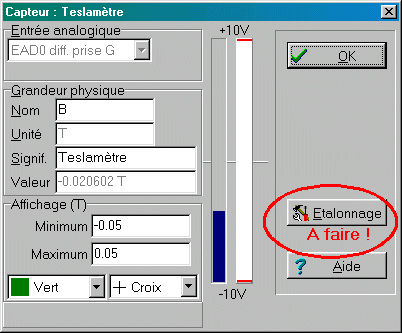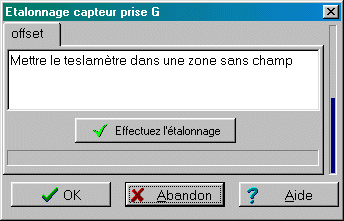
L'étalonnage s'effectue alors automatiquement: la tension de décalage (="offset") est corrigée de façon logicielle jusqu'à l'obtention du zéro.
|
NB: L'étalonnage n'est pas mémorisé par le système: il doit être repris à chaque branchement du capteur et/ou à chaque nouvelle session du logiciel d'acquisition.
C. Le capteur teslamétrique: ancien capteur M10416 avec prise din 6 broches
(pour le nouveau capteur à prise DB 15 broches, voir paragraphe précédent)
1. Présentation et mise en oeuvre
 |
ancien modèle SONDE TESLAMÉTRIQUE |
N.B.: avec GTI2 ou GTS2, l'adaptateur teslamétrique (pour prises G ou H) est indispensable |
 |
|
|
| Ce réglage de zéro demande à être repris plusieurs fois en cours de mesures (par exemple toutes les 10 mesures). |
| Le sens choisi pour placer la sonde conditionne le signe avec lequel est mesuré B. |
2. Visionner le branchement du teslamètre et le réglage du zéro
|
Penser à brancher
les haut-parleurs! |
D. Paramètres d'acquisition
L'acquisition doit cette fois se déclencher automatiquement à l'approche de l'aimant, et durer juste le temps du passage de l'aimant à travers la bobine: une synchro sur l'apparition de e est donc préférable à une synchro manuelle. La f.é.m. étant nettement plus importante, il faut changer le calibre de l'entrée analogique
Abscisse: |
Voies actives: |
Enregistrement: |
Déclenchement (synchro): |
|||||
t |
EAx: |
Variable: |
Signe: |
Cal: |
Unité: |
Nombre points: |
Durée: |
(Clavier ou clic sur bouton) Seuil: EA D1 70 mVou Seuil avec pré acquisition |
EAD1 |
e |
± |
2 | V |
100 |
200 ms |
||
EA Dx |
B |
± |
5 |
mT |
||||
* avec ORPHY-GTS2/GTI2: la synchro seuil n'est possible que sur la voie EAD1 (entrée différentielle): il suffit donc de remplacer dans les indications précédentes (schéma et réglages) EAx par EAD1.
* avec ORPHY-PORTABLE 2, brancher dans l'ordre: capsule ±2 V, capsule Teslamètre (±4 mT), et Synchro Analogique.
Charger l'acquisition pré réglée:
| * avec ORPHY-GTS2 | * avec ORPHY-GTI2 |
E. Protocole d'acquisition
| Lâcher l'aimant à quelques dizaines de cm au-dessus de la bobine; en fonction des résultats, corriger éventuellement la calibre de l'entrée analogique et la durée d'enregistrement |
| Tester avec des hauteurs de chute initiales différentes |
| Recommencer les mêmes expériences avec un nombre de spires différent (par exemple du simple au double si la bobine comporte une prise médiane) |
Ä t,
e et 
.
Dans la fenêtre 'Graphiques' (menu Fenêtre/graphe Variables),
cliquer-D pour choisir 'Coordonnées' dans le menu contextuel, ou cliquer-G sur l'icône
correspondante :
| t en abscisses |
| e en ordonnées (à gauche) |
On a ainsi la représentation graphique de e = f(t). On peut déjà visualiser ses variations, et en faire une première interprétation:
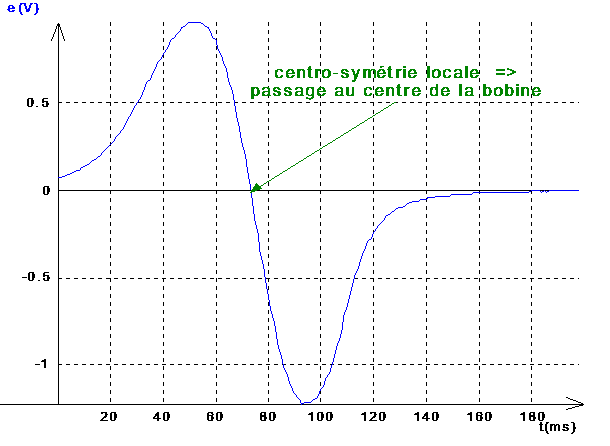
| le signe de la f.é.m. s'inverse lorsque l'aimant franchit le centre de la bobine |
| le maximum de  est plus important dans la
deuxième phase, c'est à dire lorsque la vitesse de l'aimant est plus élevée; d'où
l'idée que la valeur de dépend de la
rapidité des variations du champ magnétique vu par la bobine. L'étude quantitative
suivante va permettre de préciser ces pistes et de valider les lois de Faraday et de
Lenz. |
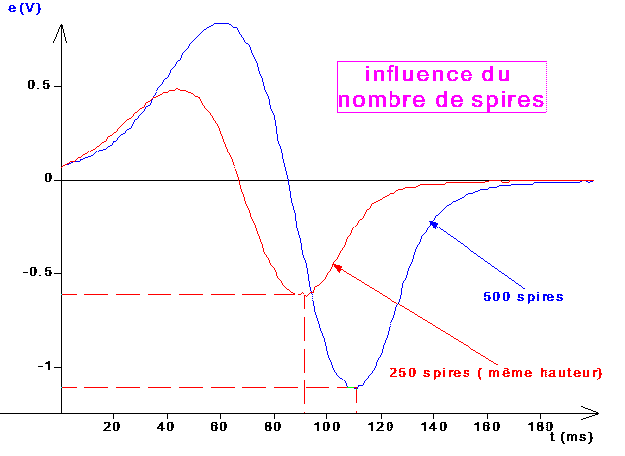
1. Comparaison de différentes pages d'acquisition: rôle du nombre de spires
Il s'agit de comparer entre deux pages d'acquisition, avec une hauteur de chute identique, le résultat obtenu avec des nombres de spires différents: par exemple la totalité de l'enroulement ou la moitié seulement (avec une bobine comportant une prise médiane)
| Choisir d'abord (Fen. Graphiques / Coordonnées ) une seule
ordonnée de façon à revenir à une seule représentation à l'écran: e(t).
Toujours dans la Fenêtre 'Graphiques', cliquer-D et choisir dans 'Coordonnées' ou
'Options': 'Superposition des pages(2)'. On
peut ainsi comparer l'aspect des différentes courbes entre elles, et discuter
qualitativement de l'incidence du nombre de spires |
| Une légende distinguant chaque courbe est ajoutée automatiquement avec l'icône  "Identification pages" ou le menu contextuel (clic-D /
Identifier pages): choisir ici N comme paramètre dans les options d'identification; il
n'y figure que si il a été déclaré comme paramètre dans le module d'acquisition (et
transféré), ou bien créé dans Regressi. Sinon, cliquer sur l'icône  et renseigner la boîte de dialogue qui s'ouvre en cochant 'paramètre
expérimental' et en indiquant N; le commentaire apparaît dans l'onglet 'Expressions'
précédé du signe ', et une nouvelle colonne dans l'onglet 'paramètres', où il n'y a
plus qu'à saisir manuellement la valeur de N page par page en fonction du nombre de
spires utilisées Cocher éventuellement les commentaires dans la même boîte pour les faire figurer dans la légende d'identification de chaque courbe (ce commentaire de page est modifiable à tout instant dans la ligne de saisie où il apparaît à droite de la barre principale d'icônes de la fenêtre logicielle) |
| Le 'curseur texte' permet d'ajouter un commentaire commun à toutes les courbes du graphique: cliquer-G sur ce nom dans la liste déroulante des curseurs, cliquer-G sur le graphique, positionner la lettre "A" apparue en glissant puis relâchant le pointeur à l'emplacement choisi pour le commentaire, saisir dans l'onglet 'texte' de la boîte qui s'ouvre automatiquement le commentaire; dans l'onglet 'options', choisir entre les différentes présentations possibles avant de valider. Ce commentaire peut à tout moment être déplacé par cliquer-glisser du pointeur dessus, ou édité par double clic-G |
| pour comparer les deux extrema, le curseur 'Réticule' permet d'inscrire (par frappe de la barre d'espace, ou double-clic) des lignes de rappel, et de lire exactement les coordonnées du point en bas de la fenêtre; un clic-D (pour choisir 'Tableau valeurs') permet alors d'accéder au tableau de leurs coordonnées, dans lequel une petite liste déroulante permet également de choisir a posteriori l'aspect de ces lignes de rappel |
| le programme calculant automatiquement l'échelle de façon à utiliser
toute la hauteur disponible sur le graphique, il faut modifier manuellement cette échelle
pour que le minimum de la courbe e(t), et donc la ligne de rappel placée par le
réticule, ne soient pas confondus avec le trait d'axe inférieur du graphique: cliquer
sur le bouton  (ou bien clic-D pour choisir
'Echelle manuelle') et imposer une valeur plus basse au minimum de e(t) dans le
tableau qui apparaît; puis valider |
| pour une même vitesse de l'aimant, on constate que la f.é.m.
d'induction est environ deux fois plus grande pour un nombre de spires double, ce qui
valide l'idée que est proportionnel au nombre
de spires N |
| une expérience identique conduite cette fois avec des inducteurs
d'aimantations différentes montrerait que est
également fonction croissante de (à sa
variation en réalité puisque en début de chute on part d'une situation où est nul). |
| Conclusion: à travers la dépendance à N
et à la variation de, on a bien vérifié que est fonction croissante de la variation du flux
embrassé par la bobine. |
|
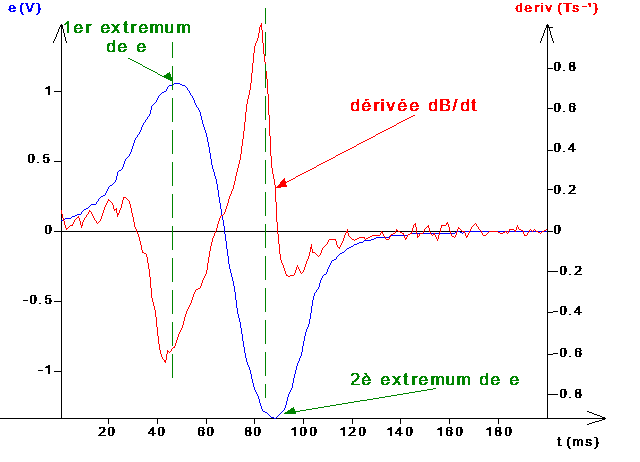
2. Rapidité de la variation du flux
Le flux reçu par la bobine varie au cours du temps avec la position instantanée de l'aimant; et de plus en plus vite au fur et à mesure de la chute de l'aimant (la vitesse de variation du flux s'accroît au cours de la chute); or le 2è extremum de
Conclusion: la f.é.m. d'induction est fonction décroissante de la durée de variation (dt) du flux.
3. Proportionnalité de la f.é.m. à dB/dt ou dF/dt
Pour vérifier véritablement la loi de Faraday, il faut maintenant comparer à chaque instant
| Revenir dans la fenêtre 'Grandeurs', onglet 'Expressions', et saisir directement dans une nouvelle ligne de ce 'mémo' (touche 'Entrée' pour revenir à la ligne, comme dans un traitement de texte): |
deriv = DIFF(B,t) (3)
pour créer la nouvelle grandeur deriv (dérivée de
; le résultat apparaît alors dans l'onglet 'Variables'.
| Dans la fenêtre 'Graphiques' (menu Fenêtre/graphe Variables), clic-D pour choisir
'Coordonnées' dans le menu contextuel, ou clic-G sur l'icône correspondante , pour ajouter l'ordonnée : |
deriv
(à droite, puisque dans une unité différente, ce qui implique un autre axe avec une autre échelle)
| Observer les concordances entre les deux courbes |
| Conclusion: On voit que (à un petit décalage temporel près dû au fait que le capteur teslamétrique n'était probablement pas tout à fait dans la zone centrale de la bobine) il y a bien:
|
Le flux étant proportionnel à , on vient de vérifier en fait que dans la relation
entre e et 
il y a bien:
** proportionnalité entre ces grandeurs (loi de Faraday)
** opposition de signe entre elles (la loi de Lenz exprimant l'opposition entre
cause et conséquence).
retour sommaire chapitre en cours
qui surgit à ce moment permet de
sélectionner seulement certaines pages parmi toutes celles du fichier.
(3) Cliquer
sur l'icône 
pour connaître la syntaxe des fonctions dans
Regressi