CHUTE LIBRE (avec MAGNUM)
II Matériel et montage
III Acquisition (avec GTI, ou GTS2, ou Orphy portable2)
IV Exploitation dans Regressi
V Étude énergétique
I Objectifs
|
 |
II Matériel et montage
A. Principe du matériel utilisé
1. Le capteur
 |
<== La fourchette optique réf. M12P205 est un capteur DB15 à reconnaissance automatique par le logiciel d'acquisition consulter la fiche technique du capteur Micrelec
|
|
Il existe une version ancienne de ce capteur (réf M10633) sans reconnaissance automatique ==> consulter la fiche technique du capteur Micrelec
|
 |
Ces capteurs utilisent tous les deux un codeur incrémental: lire le principe de ce codeur.
2. La mise en œuvre du capteur DB15 à reconnaissance automatique
Visionner l'ensemble:
|
Penser à brancher les haut-parleurs! |
|
(1) =>BRANCHER LE CAPTEUR DB15 SUR N'IMPORTE LAQUELLE DES PRISES G, H (I, J) DISPONIBLES |
|
=> (2) LE CAPTEUR EST INSTANTANÉMENT RECONNU SUR L'ÉCRAN DU LOGICIEL D'ACQUISITION:
|
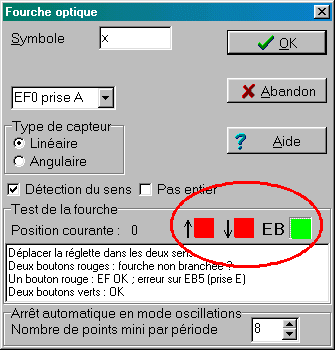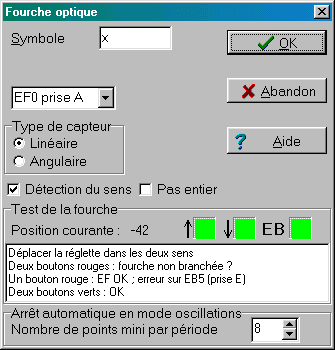
POUR VÉRIFIER LE BON FONCTIONNEMENT DU CAPTEUR, IL ET ALORS VIVEMENT CONSEILLÉ DE RÉALISER LE TEST SUIVANT:
| (1) déplacer la réglette dans les deux sens: | (2) les TROIS carrés doivent passer au vert: |
 |
 |
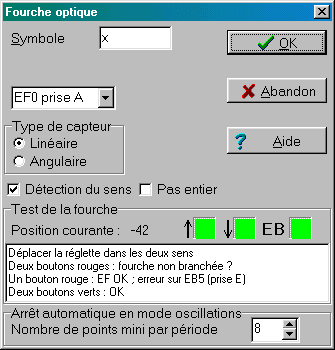NB: Précaution indispensable:
NB: Si vous avez l'habitude d'utiliser la platine de raccordement sur Orphy, il faut débrancher préalablement la nappe de liaison à Orphy, ou tout au moins s'assurer que l'interrupteur de "synchronisation" EF0/EF1 est sur la position neutre 'Arrêt'.
3. Son principe de fonctionnement (pour ceux qui veulent tout comprendre!)
|
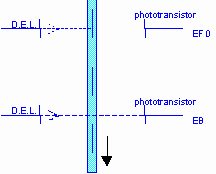
La fourchette optique de Magnum utilise un capteur bi-faisceaux: pour chacun d'eux, une diode émettrice envoie un faisceau infrarouge en direction d'un capteur (phototransistor). Le passage d'un barreau opaque de la réglette occulte le faisceau.
Le logiciel synthétise l'ensemble des 2 informations, pour compter le nombre de barreaux qui ont défilé. Le produit par le pas de 1.8 mm (et non pas 3.6, car comptage identique des fronts montants et descendants) donne l'abscisse x. Le comptage simultané du temps permet de fournir t à chaque arrivée de barreau. |
 |
|
pour plus de détails, voir la fiche détaillant le principe de ce codeur incrémental |
B. Mise en place
 |
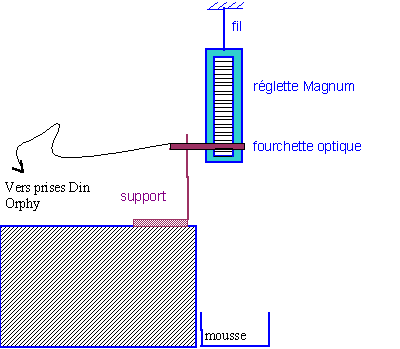Installer la fourchette optique en position horizontale sur son support, au bord d'une table, pour laisser tomber dans le vide le mobile (réglette transparente de Magnum); disposer au pied un carton avec de la mousse pour amortir le choc de la réception de la réglette. Maintenir le mobile par un fil permettra de le lâcher sans risque d'effet sur sa vitesse initiale: couper, ou mieux, brûler le fil, pour déclencher le mouvement. La flèche gravée à l'intérieur d'une des deux dents de la fourchette optique indique le sens positif des déplacements considéré par le logiciel, mais pas nécessairement celui des mouvements réels. Raccorder la fourchette optique aux prises A et E, en vérifiant bien que l'entrée front EF0 d'Orphy n'est pas raccordée par ailleurs: désactiver EF0 sur l'inverseur déclencheur du module de raccordement, ou débrancher carrément ce module de raccordement. |
C. Précautions
|
NB: Si vous avez l'habitude d'utiliser la platine de raccordement sur Orphy, il faut débrancher préalablement la nappe de liaison à Orphy, ou tout au moins s'assurer que l'interrupteur de "synchronisation" EF0/EF1 est sur la position neutre 'Arrêt'
|
 |
III Acquisitions avec Regressi pour GTI, portable2 ou GTS2
A. Réglages
 |
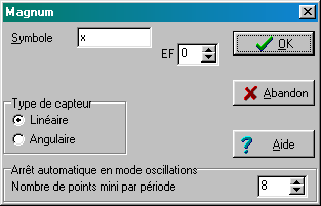Dans l'écran du logiciel d'acquisition (GTI ou GTS2), cliquer (en haut à droite de l'écran) sur la petite zone active "Mode d'acquisition", puis cocher "Magnum" dans la boîte de dialogue; valider. Cliquer sur la petite zone active "Fourchette optique" (en haut à droite) pour ouvrir la boîte de configuration de Magnum; bien vérifier que l'entrée active(0) est EF0 (c'est la seule qui soit raccordée à Orphy dans la prise din A), renommer éventuellement la variable d'acquisition; a, q, etc. (inutile de choisir le nombre de points par période). Valider. |
B. Acquisitions
|
|
Charger l'acquisition pré réglée:
| * avec ORPHY-GTS2 | * avec ORPHY-GTI |
| * avec Orphy USB ou Portable2 | |
C. Transfert
 | Cliquer sur 
pour transférer les données vers Regressi |
| dans la fenêtre "Grandeurs" de Regressi (à ouvrir avec  ),
on dispose alors dans l'onglet "Variables" d'un tableau à 2 variables: t, et x ;
observer leurs valeurs.
|
IV Exploitation dans Regressi
A. Remarques sur le dispositif d'acquisition
|
 |
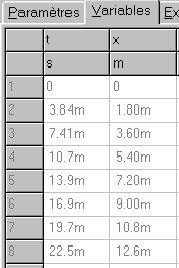B. Nature du mouvement
| En observant le tableau, comment peut-on montrer que le mouvement est accéléré? |
| Comment montrer que l'accélération est constante? |
Conclure sur la nature du mouvement (type de loi horaire).
Une première détermination de l'accélération peut alors être déduite du tableau du tableau, l'autre le sera ensuite par modélisation.
C. Modélisations de x(t)
1. Graphique des variations de x(t)
Dans la fenêtre 'Graphiques' 
,
observer les variations de x(t) pour constater que la pente n'est pas
constante. Des points erronés, en début ou fin d'acquisition, peuvent être
supprimés directement dans le graphique (sélection par clic-G, puis frappe de
la touche "Suppr"), ou après mise en sur brillance dans le tableau de
valeurs ( puis touche "Suppr", ou clic-G sur icône 
).
2. Modélisations des variations de x(t)
Cliquer-D pour choisir 'Modélisation' dans le menu
contextuel, ou cliquer-G sur l'icône correspondante 
,
ou frapper touche F9: un volet supplémentaire s'ouvre alors dans la
partie gauche de la fenêtre graphique. Saisir dans la zone "Expression du
modèle" le type de fonction choisie.
|
Il peut être intéressant de ne pas donner tout de suite aux élèves la bonne solution, mais de leur faire comparer les modèles linéaire et parabolique. Saisir pour cela: x=0.5*g*t^2+b*t+c et valider par l'icône de mise à jour |
|
,
ou touche F2, ou double frappe de la touche Entrée Demander au logiciel d'ajuster (clic-G sur le bouton
"ajuster" 
)
le modèle à la courbe expérimentale en calculant la valeur des paramètres
figurant dans l'équation du modèle:
N.B. L'ajustage est automatique dans le cas du modèle affine si ce choix a été coché dans l'onglet 'Modélisation' du menu 'Options'.
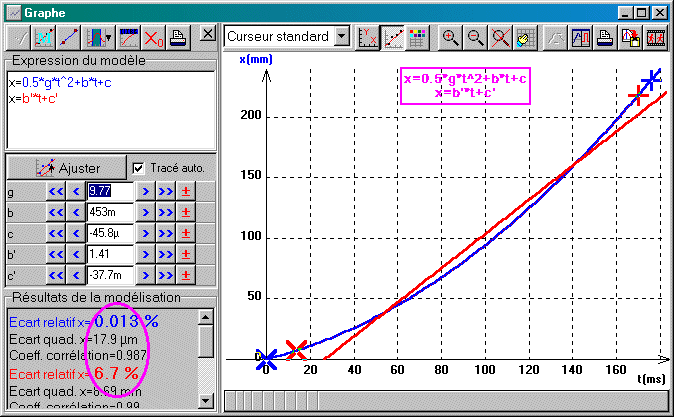
| Comparer les écarts relatifs modèle/expérience indiqués dans chaque cas par le logiciel, et valider ainsi le choix du modèle parabolique. On obtient une valeur expérimentale de g très proche de la valeur optimale: ici 9.77 m/s². |
On peut utiliser en place de saisie manuelle des modèles
prédéfinis (2) (accès par clic-G sur icône correspondante 
):
dans ce cas, le modèle proposé porte uniquement sur la première variable
située sur l'axe de gauche.
D. Calcul et modélisation de v(t)
1. Calcul de la dérivée
Les nouvelles variables (au sens de Regressi, en réalité elles-mêmes fonctions d'autres variables) se créent dans la fenêtre "Grandeurs", dans l'onglet "Expressions", à la suite des commentaires importés de l'acquisition:
| Dans l'onglet "Expressions", saisir avec la syntaxe (3) de Regressi: |
v=diff(x, t)
| Dans la fenêtre "Graphiques", faire afficher le
graphe des variations de v(t): cliquer-G sur l'icône  ,
et ajouter
une 2è ordonnée v, à droite, puis valider. Remarquer que cette fois-ci la représentation graphique est rectiligne. |
2. Modélisation
Revenir à la modélisation dans la fenêtre "Graphiques". Saisir dans la zone "Expression du modèle" le type de fonction choisie sous la forme:
v=a*t+v0
et valider par l'icône de mise à jour 
.
On obtient une nouvelle détermination expérimentale de g très proche
de la précédente.
V Étude énergétique
Ces nouvelles variables se créent comme précédemment dans la fenêtre "Grandeurs" (onglet "Expressions"). Commencer par saisir la valeur de la masse du mobile, avec son unité:
m=0.031_kg
et valider de la façon habituelle ( ,
ou F2, etc.). La masse devient ainsi un paramètre global, réutilisable
dans des formules littérales avec l'unité S.I., à n'importe quelle page du
fichier Regressi ouvert.
A. Énergie cinétique
Saisir sur une nouvelle ligne (saut de ligne par touche "Entrée") du "mémo":
Ec=½*m*sqr(v)
3Après validation, la variable correspondante remplit une nouvelle colonne dans l'onglet "Variables".
B. Énergie potentielle
|
Celle-ci n'est définie qu'à une constante près, dépendant du niveau choisi comme référence. Si on choisit par exemple celui situé à 30 cm en dessous du niveau de départ, saisir sur une nouvelle ligne du "mémo": Ep=m*9.81*(0.3-x) et mettre à jour. L'unité de g = 9.81 m/s² étant inconnue du logiciel, il faut passer dans l'onglet "Incertitudes/Unités" pour indiquer manuellement l'unité de Em; à moins d'avoir déclaré initialement g comme paramètre global avec son unité (comme on l'a fait plus haut pour m). |
 |
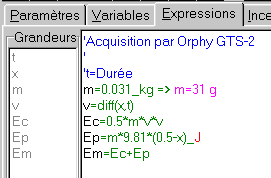C. Énergie mécanique
Rentrer alors:
Em=Ep+Ec
pour créer la variable d'énergie mécanique. Observer dans le tableau des variables les variations éventuelles de l'énergie mécanique (cas de frottements parasites contre la fourchette), ou sa constance (en général très bien vérifiée, grâce à la forme aérodynamique du mobile utilisé).
D. Visualisation graphique
Passer dans la Fenêtre "Graphiques" et demander par la boîte "Coordonnées" l'affichage des ordonnées Ep, Ec, et Em à gauche, en choisissant éventuellement d'afficher x ou v sur l'axe de droite.
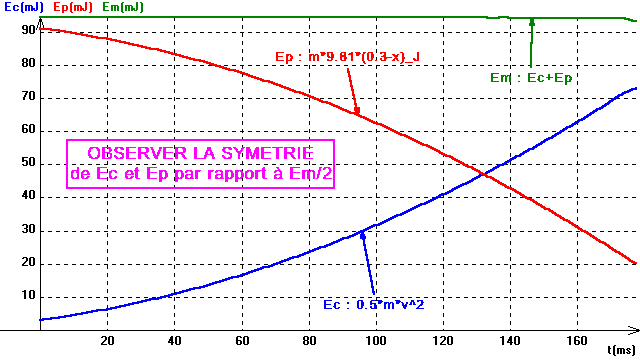
On voit alors très bien l'effet de "vase communiquant" d'énergie entre les formes potentielle et cinétique au cours du mouvement. L'énergie mécanique reste bien constante sur la durée de l'expérience (l'énergie dissipée par les frottements est ici négligeable par rapport à l'ordre de grandeur de l'énergie totale).
Passer dans la Fenêtre "Graphiques" et demander dans la boîte
"Coordonnées" ou 
l'affichage
d'ordonnées supplémentaires pour Ep, Ec, et
Em à gauche, en choisissant éventuellement d'afficher x ou v sur l'axe
de droite. On voit alors très bien l'effet de "vase communiquant" d'énergie
entre les formes potentielle et cinétique au cours du mouvement. L'énergie mécanique
reste bien constante, sauf pour les petites valeurs d'angles: l'énergie dissipée par les
frottements y devient moins négligeable par rapport à l'ordre de grandeur de l'énergie
totale.
(0) choix possible seulement dans les versions anciennes de Regressi (avant été 2002); dans les versions plus récentes, EF0 est imposée par le logiciel, et le choix n'apparaît plus dans la boîte de dialogue.
(1) La simple frappe de cette touche effectuant un saut de ligne, comme dans un traitement de texte.(2) accessibles seulement si ce choix a été coché dans l'onglet 'Modélisation' du menu 'Options'.
(3) Consulter l'aide sur la syntaxe par l'icône
.