II Exemple choisi: résonance d'un circuit R-L-C
III Création de la première page du fichier
IV Étude de la largeur de bande passante à –2 dB
V Influence de l'amortissement sur l'acuité de la résonance
VI Généralisation de la méthode de simulation
I Objectifs
Cette approche par simulation est intéressante surtout pour les courbes aux formes exotiques, ou difficiles à tracer manuellement avec précision. |
 |
II Exemple choisi: résonance d'un circuit R-L-C
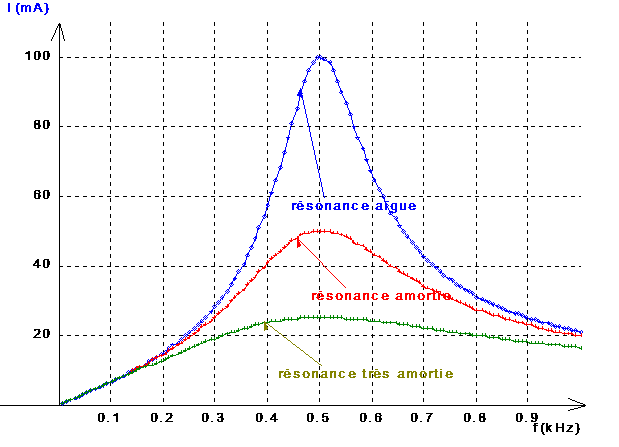
Nous voulons par exemple faire tracer ici les courbes de résonance classiques I=f(f) de l'intensité du courant dans un circuit R-L-C série alimenté sous une tension de valeur efficace U constante. Cela pour différentes valeurs de l'amortissement (terme R).
Après que cet exemple ait été détaillé, d'autres idées d'application de l'outil sont proposées à la fin du chapitre.
III Création de la première page du fichier
 | Commencer par demander Fichier / Nouveau / Simulation, et renseigner l'onglet 'Expressions' dans la fenêtre 'Grandeurs' qui s'est ouverte automatiquement:
| ||||||
| Il faut ensuite rentrer dans la zone inférieure du même onglet l'expression de la fonction I=f(f), mais pour éviter des messages d'erreur éventuels, il vaut mieux commencer par indiquer au programme les valeurs numériques des paramètres L, C, U, et R en les saisissant ligne par ligne dans le 'mémo' du même onglet (touche 'Entrée' pour le saut de ligne) avec la syntaxe suivante: |
L=0.1_H
où l'unité de chaque paramètre peut être saisie directement à la suite de sa valeur à condition d'utiliser le trait de soulignement "_" comme séparateur (vérifier dans l'onglet "Incertitudes / Unités" que les unités ont bien été ainsi importées automatiquement).
| Saisir ensuite dans une nouvelle ligne de ce 'mémo' l'expression classique I=f(f): |
où w = 2*p*f, ce qui donne dans la syntaxe(1) de Regressi:
I=U/(sqr(R)+(L*2*p*f-1/(C*2*p*f))^2)^(1/2)
ou bien (utilisation des nombres complexes) plus succinctement:
I=U/abs(R+j*L*2*p*f+1/(j*C*2*p*f))
Valider par la touche 'F2' ou en cliquant-G sur l'icône
clignotante 
; le résultat
apparaît alors dans l'onglet 'Variables', en même temps qu'on obtient la représentation
graphique de I=f(f).
IV Étude de la largeur de bande passante à –3 dB
Elle se fait facilement sur le graphique en choisissant le curseur 'Données': dans sa boîte de dialogue, cocher seulement:
| abscisse |
| ordonnée |
| écart |
puis déplacer le pointeur de façon à amener le petit segment qui est
apparu sur le graphique jusqu'à l'ordonnée 
(la valeur courante de l'ordonnée s'affiche en dessous); on lit alors en dessous du
graphique la largeur de bande sous la forme:
V Influence de l'amortissement sur l'acuité de la résonance
Il s'agit de créer d'autres pages représentant la même fonction, mais avec d'autres valeurs du paramètre R. Il faut d'abord changer le statut de R de "paramètre global" (=constante) en "paramètre de page (2)":
A. Création du paramètre de page
|
 |
Deux méthodes s'offrent:
| Demander alors (menu principal): 'Page nouvelle', et donner une nouvelle valeur à R dans l'onglet 'Paramètres' pour cette page n°2: le graphique correspondant s'affiche automatiquement |
| Plus rapidement, saisir la nouvelle valeur de R dans la deuxième ligne du tableau de l'onglet "Paramètres". |
Comparer les courbes des deux pages entre elles
en demandant la superposition des deux graphiques (clic-D sur fenêtre 'Graphique':
choisir 'Coordonnées' ou 'Options 
')
| Ajouter une légende pour chaque courbe automatiquement en cliquant-D sur le
bouton 'Identification pages' (juste à droite de celui d'échelle manuelle); la boîte
d'options d'identification qui s'ouvre propose d'inclure dans la légende de chaque
courbe:
|
| Après application de la légende, chacune des étiquettes est repositionnable indépendamment par cliquer glisser du pointeur qui se transforme en main. |
E. Étude du maximum d'amplitude à la résonance en fonction de l'amortissement
| Créer la variable 'Imax' (=maximum de la valeur efficace) en saisissant dans une nouvelle ligne du 'mémo' de l'onglet 'Expressions': |
Imax= max(I)
| Observer dans l'onglet 'Paramètres' le résultat pour les valeurs de Imax en fonction de celles de l'amortissement R |
| La représentation graphique correspondante s'obtient dans la fenêtre 'Graphe paramètres' (icône sous la barre de menus principale, ou menu 'Fenêtres') |
| On peut alors y faire la modélisation de Imax = f(R) par un modèle de type hyperbolique; on vérifiera ainsi que I =U/R à la résonance (impédance du circuit égale à la seule résistance ohmique). |
VI Généralisation de la méthode de simulation
Ces possibilités de Regressi en mode 'traceur de courbes' peuvent être étendues à de nombreux domaines; même à celui de fonctions fournies sous la forme d'équations différentielles (voir documentation accompagnant le logiciel). Ce paragraphe vise à donner une idée de la variété des applications possibles.
A. Synthèse de Fourier(voir à ce sujet les articles parus dans les n° 771 et
773 du B.U.P.).
On peut par exemple superposer les 4 premiers harmoniques de rang impair dans la
composition d'un signal "créneau".
 |
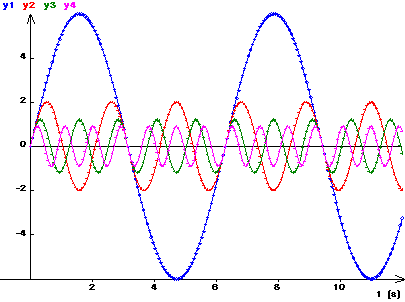fondamental et harmoniques: y1 = 6*sin(t) y2 = 2*sin(3*t) y3 = 1.2*sin(5*t) y4 = 0.9*sin(7*t) |
 |
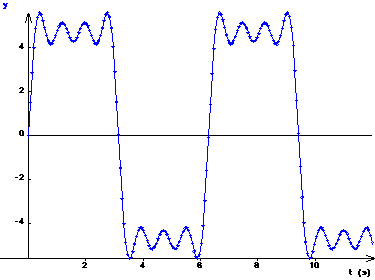signal composé: y = y1+y2+y3+y4 |
Le signal obtenu ainsi par synthèse a déjà fortement l'allure d'un signal "créneau".
| L'appel de la fenêtre Fourier permet, en partant de y(t), de retrouver par décomposition les fréquences et les amplitudes des harmoniques (et de constater en même temps les limites ou les contraintes à respecter pour cette méthode). Dans le spectre ci-contre, on a demandé à Regressi l'abscisse en "fréquence réduite" parmi les options de transformée de Fourier dans la fenêtre Fourier (dans cet exercice de simulation, les valeurs en hertz n'ont pas d'importance). |  |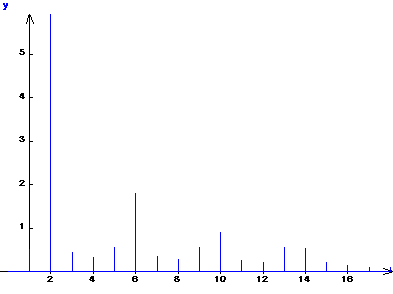
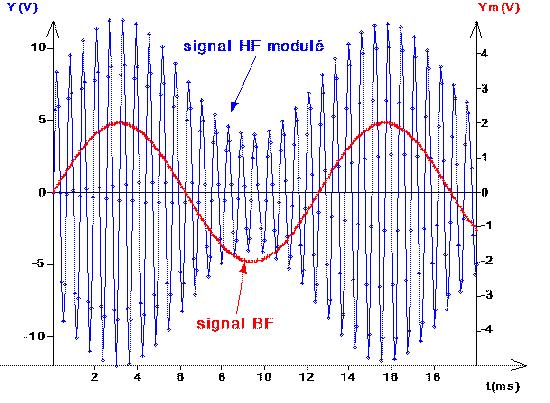
On obtient facilement la représentation de la porteuse, du signal B.F. (= modulant), et du signal modulé, en saisissant les équations indiquées ci-dessous:
| MODULATION D'AMPLITUDE: | |
Yp=2*sin(10000*t) Ym=Vm*sin(500*t) Y1=Ym+V0 Y=Yp*Y1 'Vm=amplitude B.F.
en indiquant dans l'onglet "Paramètres": V0 = 4 V Vm = 2 V |
 |
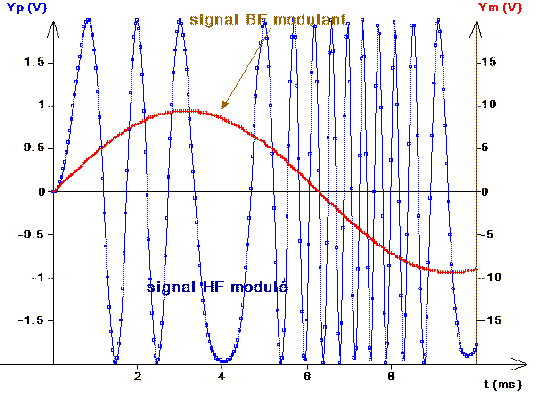
MODULATION DE FREQUENCE: |
|
Ym=m*47*sin(500*t) Yp=2*sin(500*Ym*t)
en indiquant dans l'onglet "Paramètres": |
 |
C. Fonction définie à partir de son équation différentielle et de conditions initiales: étude du régime oscillant d'un circuit R-L-C
1. Présentation
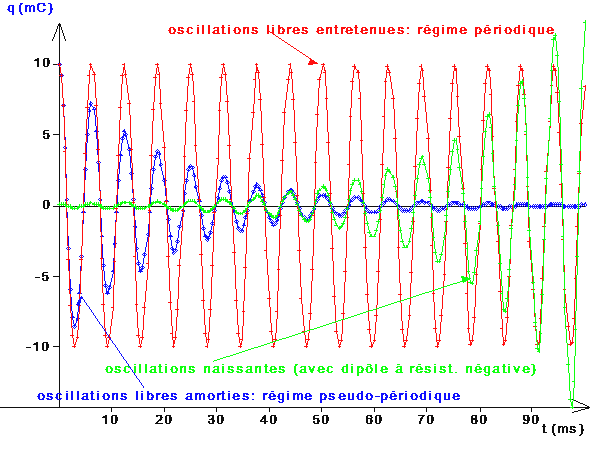
L'équation différentielle d'un circuit R-L-C série peut s'écrire:q''=-(Ro/L)*q'-(1/(L*C))*q
| Si Ro > 0, on a un régime d'oscillations amorties |
| Si Ro < 0 (montage dit "à résistance négative", par exemple avec un amplificateur opérationnel), on a des oscillations croissantes (tout au moins dans les limites de la linéarité du montage) |
| Dans le cas limite Ro = 0, les oscillations sont entretenues avec une amplitude constante. |
2. Simulation
On vise à obtenir le graphique de synthèse suivant:
Pour simuler ces différents régimes, il suffit de:
|
|
| Pour créer les autres pages pour les nouvelles valeurs de Ro, il suffit de saisir sur une nouvelle ligne de l'onglet "Paramètres" les autres valeurs de Ro: |
Ro = 0
Ro = -100
sans oublier de re donner pour ces nouvelles pages les valeurs des conditions initiales pour q et q'. Les pages correspondantes sont alors créées en même temps, et le graphe actualisé.
D. Résolution d'un exercice de Physique: adaptation d'impédance
1. Présentation de l'exercice à résoudre: adaptation d'impédance
 |
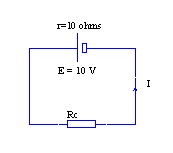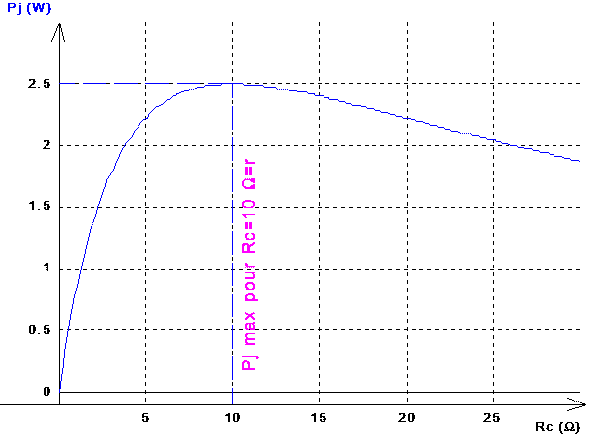
Un générateur de caractéristiques (E, r) connues fournit par effet Joule de la puissance électrique à une charge purement résistive Rc. Il s'agit pour les élèves de découvrir pour quelle valeur de Rc la puissance Pj transférée du générateur au résistor est maxima. C'est l'exercice classique d'adaptation d'impédance(3) du récepteur au générateur (ou vice-versa). Les grandeurs E et I pourront indifféremment représenter des valeurs continues (choix effectué ici) ou des valeurs efficaces (avec un générateur de tension alternative dans le schéma), suivant le cadre dans lequel on décide de traiter le problème. |
2. Mise en équation et formulation graphique
Il suffit d'exprimer en fonction de Rc (paramètre du problème) la puissance Pj dissipée dans Rc et de chercher quand Pj est maxima:
 | L'intensité est donnée par la loi de Pouillet:  |
| la puissance calorifique s'en déduit par la loi de
Joule:  |
| on va donc chercher si la fonction Pj = f(Rc) possède un maximum, et pour quelle valeur de Rc (E, et r étant connus), en représentant ses variations sur l'intervalle {0, 3*r}, c'est à dire {0, 30 W }. |
3. Création des grandeurs et paramètres
|
|
Création des paramètres Rc et r: saisir directement sur deux lignes successives (touche 'Entrée' pour le changement de ligne) dans l'onglet 'Expressions' de la fenêtre 'Grandeurs' les expressions:
E=10_V
r=10_E=10_V
r=10_W
en respectant bien le trait
Ces paramètres auraient pu être créés d'une autre manière après clic-G sur l'icône : dans la boîte de dialogue qui s'ouvre, choisir 'Paramètre expérimental' et remplir les différents champs (nom et unité)
Création et visualisation de Pj: sur une nouvelle ligne, saisir l'expression définissant Pj:
Pj= Rc*sqr(E) / sqr(Rc+r)
La validation de la saisie précédente (F2 ou Vérifier sur l'étiquette d'axe que l'unité de Pj a bien été générée automatiquement; sinon, cliquer sur le bouton ou la saisir manuellement dans l'onglet 'Unités' de la fenêtre 'Grandeurs'
Penser à faire une sauvegarde de l'ensemble de ces informations.
4. Étude purement graphique
Observer les variations de Pj sur son graphique: cette grandeur passe par un maximum dont l'abscisse Rc semble avoir la même valeur que r (10 W ici). Pour valider cette hypothèse, il faut bien sûr qu'elle soit corroborée par d'autres valeurs de r: modifier manuellement la valeur du paramètre r dans l'onglet 'Expressions': essayer d'autres valeurs numériques, en modifiant au besoin la valeur du maxi pour la variable de contrôle. On peut alors conclure empiriquement sur la condition d'adaptation d'impédance Rc = r.
On peut éditer le graphique avec divers outils pour mettre en évidence cette propriété:
| Le curseur 'réticule' se déplace au gré du pointeur, et ses coordonnées courantes sont affichées en permanence en bas de la fenêtre graphique: lire l'abscisse du maximum de Pj. De plus, pour une position donnée du réticule, la frappe de la barre d'espace a pour effet de marquer(5) le graphique à l'emplacement du réticule. Un tableau de valeurs local, accessible par clic-D sur la fenêtre 'Graphique', récapitule toutes les valeurs de coordonnées qui ont été marquées ainsi à partir du curseur 'réticule'; la boîte comportant le tableau permet aussi d'éditer l'aspect des lignes de rappel marquées à partir du curseur |
| Le curseur 'Texte' permet d'ajouter un commentaire le long de cette ligne (en cochant par exemple le choix 'vertical' dans l'onglet d'options de ce curseur pour arriver au résultat ci-joint) |
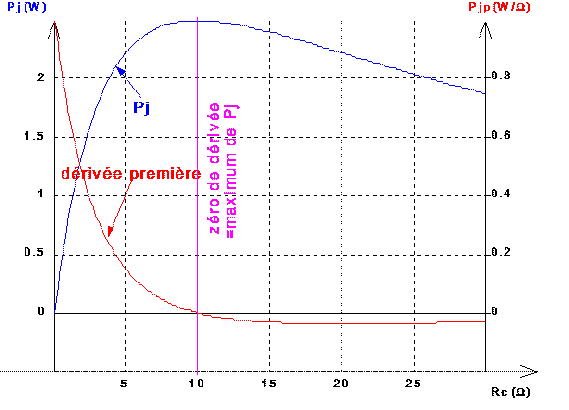
5. Étude algébrique avec la dérivée
|
|
| Passer à la fenêtre 'Graphique' et choisir les tracés de
variables à superposer, après clic-G sur l'icône
|
(ou choix 'Coordonnées' dans le menu contextuel ouvert par clic-D): | Ajouter des légendes au graphique comme dans le paragraphe précédent: |
| Le curseur 'Ligne' trace une ligne par cliquer-glisser du pointeur: on la force à être parfaitement verticale en enfonçant la touche 'Majuscule' pendant le tracé; la ligne peut ensuite être éditée (=modifiée) par un double clic dessus, qui ouvre une boîte de dialogue dans laquelle se font les choix de motif et de couleur. |
de la Fenêtre 'Grandeurs'
(2) pour
reprendre la terminologie de la documentation de Regressi
(3) dont la réponse bien
connue est Rc = r, et cela quelle que soit r
(4) une seule frappe a pour
effet un 'retour ligne', comme dans un traitement de texte
(5) la même manœuvre
effectuée au même endroit aura pour effet d'effacer le marquage
(6) on accède à la syntaxe des fonctions dans
Regressi avec l'icône 
.