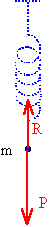OSCILLATEUR
HARMONIQUE VERTICAL:
masse suspendue à un ressort
I Objectifs
II Matériel et montage: principe et mise en oeuvre
III Exploitation de l'enregistrement dans Regressi
IV Graphe des paramètres lorsque k est connue
V Étude énergétique
N.B. : T.P. possible en utilisant le nouveau capteur Micrelec "Dynamomètre" pour prises DB15.
I Objectifs
|
 |
II Matériel et montage: principe et mise en oeuvre
|
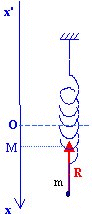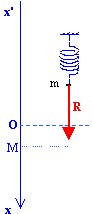
Le ressort vertical est suspendu au bras de mesure du capteur,
qui est lui-même fixé de façon rigide sur un support.
|
|
A. Principe: la tension du ressort est l'image de l'élongation
Le système choisi pour l'inventaire des forces appliquées détermine celles-ci:
|
SYSTÈME: |
Masse seule | Ressort seul |
Bras capteur support |
| Relations entre forces appliquées: | R= -k*x | T'= -T et R= -T (principe actions réciproques) |
R'= -T |
| Inventaire
des forces:
|
|
 |
 |
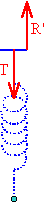D'où en conclusion:
R'= -k*x
C'est-à-dire que la réaction du support (bras du capteur de force) est en permanence l'image de l'élongation x de la masse oscillante, à une constante de proportionnalité près (k).
B. Le capteur et sa mise en oeuvre
|
Penser à brancher
les haut-parleurs! |
1. Cas du nouveau capteur (DB15) à reconnaissance auto réf M12P309
|
|
Consulter la fiche technique MICRELEC du capteur: DYNAMOMÈTRE/5 newtons pour GTI2/GTS2 |
|
(1) ==> |
|
=> (2)==>
|
2. Cas de l'ancien capteur DIN 6 broches
|
Consulter
la fiche technique MICRELEC du capteur: DYNAMOMÈTRE pour GTI/GTS2
|
 |
 |
Sur ORPHY GTI2, les prises DIN 6 broches repérées A à F n'existent plus: il suffit alors de brancher l'adaptateur DIN pour GTI2 réf M12G504 pour disposer de ces prises (sur lesquelles se branche le module Transel, l'ancien module de pression, etc). |
C. Le ressort; étalonnage manuel préalable avec Regressi
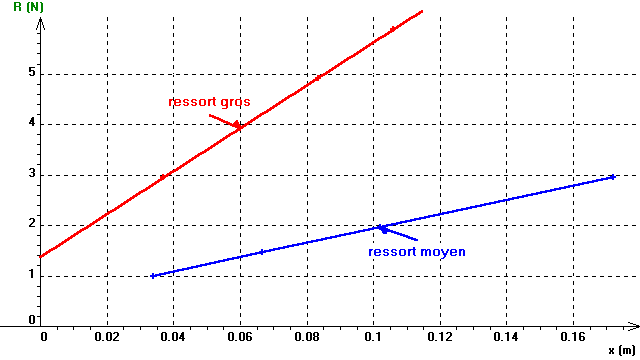
Il s'agit de tracer la courbe d'étalonnage du ressort R= f(x), pour en déduire sa constante de raideur k par une modélisation dans Regressi.
1. PrincipeOn mesure l'allongement x= OM du ressort pour différentes valeurs de la masse m suspendue à son extrémité: un traitement dans le tableur REGRESSI permet ensuite de déduire l'intensité du poids, donc de la tension R en fonction de x. 2. Saisie dans REGRESSI et calcul de la tension RLes valeurs de m et x sont saisies manuellement dans
REGRESSI: ouvrir la session avec Fichier/ Nouveau/ clavier. Les
informations rentrées à ce stade (nom de variable, unité, etc.) dans la
boite de dialogue pourront être éventuellement modifiées par la suite en
double-cliquant sur la tête de colonne de chaque variable (onglet
"Variables" de la fenêtre "Grandeurs" |
 |
);
l'échelle (valeurs min/max) du graphique se modifie avec le bouton 
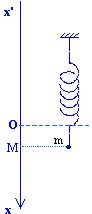. | Pour positionner côte à côte le tableau et le graphe (qui se trace au fur et à mesure), demander "Fenêtre/Mosaïque verticale"). On peut constater que pour la plupart des ressorts, qui sont à spires jointives, la ligne des points obtenus est bien rectiligne, mais ne passe pas par l'origine: il faut une certaine tension R0 pour obtenir un début d'allongement. |
| Pour un traitement plus rapide avec plusieurs ressorts,
passer au ressort suivant dans le même fichier par la commande
"Page/Nouvelle". Penser à laisser un commentaire (identification
de chaque ressort) dans la ligne de saisie correspondante (sous la barre de
boutons principale). La navigation d'une page à l'autre se fait ensuite par
les boutons     ,
ou les raccourcis F7/F8. |
| Calcul de la nouvelle variable R: fenêtre "Grandeurs"/ onglet "Expressions", saisir d'abord la constante g en indiquant sa valeur, mais en respectant bien la syntaxe de Regressi; pour la saisie de l'unité, 3 modes sont possibles: |
; le
logiciel revoie:3. Exploitation par modélisation
| Dans la fenêtre 'Graphiques', clic-D pour choisir 'Modélisation' dans le
menu contextuel, ou clic-G sur l'icône correspondante 
(ou touche F9): un volet supplémentaire s'ouvre alors dans la partie
gauche de la fenêtre graphique. Saisir dans la zone "Expression du
modèle" le type de fonction choisi sous la forme (ici fonction
linéaire):
R=k*x+R0 ce qui demande au logiciel de chercher pour quelles valeurs de
k et R0 la
courbe théorique colle au plus près des points expérimentaux. On peut
utiliser en place de saisie manuelle des modèles prédéfinis (accès par
clic-G sur icône correspondante Demander éventuellement (par exemple après avoir supprimé un point
aberrant de l'acquisition) au logiciel d'ajuster (clic-G sur le bouton
"ajuster" |  ) le
modèle à la courbe expérimentale en calculant la valeur du paramètres
figurant dans l'équation du modèle: Regressi passe automatiquement en mode
graphique 'points' (au lieu de lissage entre les points), ajuste la courbe
modèle aux points expérimentaux, et ajoute dans l'onglet 'Paramètres' de
la fenêtre 'Grandeurs' une colonne par paramètre en y indiquant la valeur
calculée par la modélisation (valeurs des paramètres qui figurent aussi
dans la fenêtre graphique): ici k et R0. |
: dans ce cas, la modélisation porte uniquement sur la première
variable située sur l'axe de gauche.
|
|
Procéder de même dans les 2 pages (touches F7-F8 pour
changer de page, ou touches de navigation 
);
les résultats du calcul des paramètres de pages (valeurs de k et R0) sont
résumés, avec leur unité, dans l'onglet "Paramètre" de la
fenêtre "Grandeurs".
D. Le montage pour l'étude des oscillationsLe ressort est directement suspendu au bras du capteur; on considère ce bras comme immobile pendant les oscillations et les variations de la tension R du ressort.E. Réglages logiciels; acquisitionsL'écran d'acquisition est paramétré de façon à enregistrer les points R=f(t):
|
 |
Abscisse: |
Voies actives: |
Enregistrement: |
Déclenchement (synchro): |
|||||
|
Temps t |
EAx: |
Variable: |
Signe: |
Cal: |
Unité: |
Nombre points: |
Durée: |
Manuel |
EA8 |
R |
+ |
19.6 |
N |
200 |
1 à 3 s |
||
* avec ORPHY-PORTABLE 2, brancher: capsule "FORCE" M11P329.
Charger l'acquisition pré réglée:
| * avec ORPHY-GTS2 | * avec ORPHY-GTI2 |
Lancer le mouvement en écartant la masse de sa position de
repos, lâcher sans vitesse initiale, bien dans l'axe vertical du bras de
suspension, et lancer aussitôt l'enregistrement (barre d'espace, ou clic-G sur
le bouton "Acquisitions" 
). Les conditions
initiales sont donc:
| élongation initiale |
| pas de vitesse initiale. |
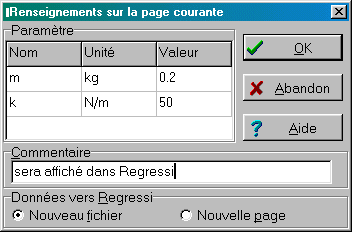
F. Transferts vers Regressi; paramètres de page
Ces valeurs des paramètres seront ensuite affichées
dans l'onglet "Paramètres" de la fenêtre
"Grandeurs" |
 |
: renseigner la boite de dialogue qui
s'ouvre en indiquant ceux des paramètres de page qui sont éventuellement
connus: m, et (ou) k.: nom, unité, valeur.
.1. Première page d'acquisition
|
On trouve dans l'onglet "Variables": Ä t et RDans la fenêtre 'Graphiques'
|
 |
(menu Fenêtre/graphe Variables), clic-D pour choisir 'Coordonnées' dans
le menu contextuel, ou clic-G sur l'icône 
,
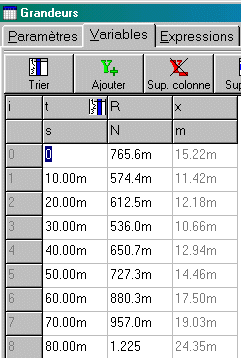pour vérifier qu'on a:2. Calcul de l'élongation (dans l'hypothèse où la valeur de k est connue)
On a ainsi la représentation graphique de R= f(t). L'amortissement se distingue nettement dès qu'on a plus d'une oscillation, ainsi que la pseudo périodicité.
 |
Revenir dans la fenêtre 'Grandeurs' x= R/k ou bien: x= (R-R0)/k pour créer la nouvelle grandeur x, et valider par la
touche 'F2' (ou double frappe de la touche 'Entrée') ou en cliquant-G
sur l'icône clignotante |
; le résultat
apparaît alors dans l'onglet 'Variables', avec son unité correcte (S.I.)On observe déjà dans les valeurs numériques de ce tableau que la correspondance avec t n'est pas du tout linéaire.
3. Pages suivantes (acquisitions transférées dans le même fichier)
Pour réaliser ensuite une première étude qualitative, on peut par exemple:
| Réaliser une 2è acquisition en conservant la valeur de m et en changeant celle de k |
| Réaliser une 3è acquisition en conservant la valeur de k et en changeant celle de m |
Procéder comme précédemment §II.E.), mais lors de l'ouverture de la boîte de renseignements sur le transfert des données vers Regressi, bien cocher "Nouvelle page", et renseigner la nouvelle valeur de l'angle. Dans Regressi, sauver au passage la nouvelle acquisition, et recommencer de même pour la 3è. Par comparaison avec la 1è page, on verra ainsi séparément sur les résultats l'influence:
| De m seule |
| De k seule. |
III Exploitation de l'enregistrement dans Regressi
Dans la fenêtre 'Graphiques' 
(menu Fenêtre/graphe Variables), clic-D pour choisir 'Coordonnées' dans le
menu contextuel, ou clic-G sur l'icône 
, pour
choisir x en ordonnée. On a alors la représentation de x= f(t).
A. Déterminations rapides de la période; amortissement
1. Amortissement
2. Période
|
 |
 |
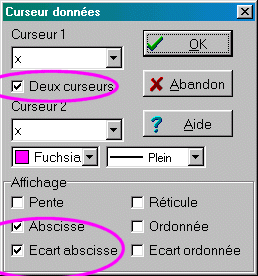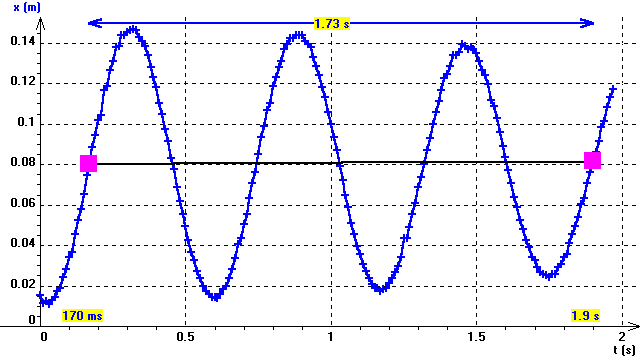
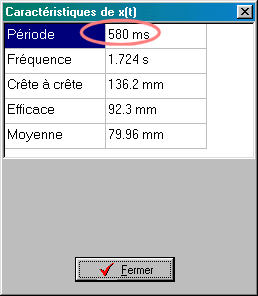On obtient ici: 3*d t= 1.73 s d'où d t= 1.73/ 3 » 0.58 s.
|
| Dans le tableau des valeurs des variables, un examen des abscisses de chaque maximum permet aussi d'en déduire la période. |
|
On procède de même dans chaque page d'acquisition, pour avoir des valeurs différentes de la période en fonction des paramètres m, ou k: les résultats sont stockés dans l'onglet "Paramètres".
|
 |
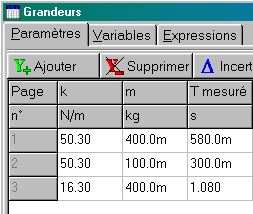B. Comparaisons qualitative et quantitative de la période entre les 3 pages d'acquisition (à m ou k égale)
1. Comparaison qualitative
On constate pour la période Tmesurée que:
| Elle croît avec m |
| Elle décroît avec k. |
Ces résultats sont cohérents avec la formule théorique:
.
2. Comparaison quantitative
Par comparaison des 3 pages d'acquisition précédentes, on obtient les résultats suivants:
| Pour l'influence de m: |
|
m |
T |
m1/m2 |
|
T1/T2 |
|
|
Page 1 |
400 g |
0.58 s |
4 |
|
2 |
|
Page 2 |
100 g |
0.30 s |
=2Ce qui vérifie:
| Pour l'influence de k: |
|
k |
T |
k1/k3 |
|
T3/T1 |
|
|
Page 1 |
50 |
0.58 s |
3.1 |
|
1.86 |
|
Page 3 |
16 |
1.08 s |
=1.8Ce qui vérifie:
On constate dans tous les cas que la formule théorique du pendule élastique
est cohérente avec ces résultats expérimentaux: elle est vérifiée avec une très bonne précision (de l'ordre de 3%).
C. Élongation, vitesse et accélération: calculs et prolongements
1. Changement d'origine pour les abscisses
|
La position d'équilibre le la masse oscillante est en fait le centre de symétrie des oscillations (donc moyenne des valeurs de x pour la calculer facilement): il est judicieux de la choisir comme nouvelle origine, pour simplifier certaines formules de l'étude, en particulier celles concernant l'élongation (modélisation au §D.) ou l'énergie mécanique. Les nouvelles variables (au sens de Regressi, en réalité
elles-mêmes fonctions d'autres variables) se créent dans la fenêtre
"Grandeurs" |
, onglet
"Expressions", à la suite des commentairesX= x-moy(x)
et valider par la touche 'F2' (ou double frappe de la touche 'Entrée') ou en cliquant-G sur l'icône clignotante
; le résultat apparaît alors dans l'onglet 'Variables', avec son unité correcte (S.I.).
Dans la fenêtre "Graphiques", cliquer-G sur l'icône
, et remplacer x(t) par X(t) pour l'ordonnée de la 1è courbe: le nouveau graphe est centré sur l'axe des temps.
2. Calculs de v et a
|
Préalable: le calcul de la dérivée seconde (a) par voie logicielle introduit une incertitude trop grande ici s'il est fait sur un trop petit nombre de points: il faut donc choisir un plus grand nombre de points: aller pour cela dans les Options de REGRESSI, onglet "Calcul", et régler le "Nombre de points utilisés pour le calcul de la dérivée" au moins à 9! Continuer dans la fenêtre "Grandeurs" |
|
,
onglet "Expressions": | Pour la vitesse: |
v=diff(X, t)
| L'accélération s'obtient par nouvelle dérivation: |
a=diff(v, t)
| Dans la fenêtre "Graphiques", ajouter le graphe des variations
de v(t): cliquer-G sur l'icône  ,
et ajouter à x(t) une 2è courbe (ordonnée v, à droite),
puis valider. On peut alors observer le déphasage (quadrature avance).
|
3. Étude des déphasages de v(t) et a(t) par rapport à x(t)
Visualiser simultanément le déphasage de v(t) et
a(t) par rapport à X(t) nécessite de recourir à l'affichage
côte à côte de deux graphiques: dans la fenêtre 'Graphiques' 
,
cliquer-G sur l'icône 'Deux graphes' 
(qui reste
enfoncée tant que ce mode est actif), ou cliquer-D pour choisir dans le menu
contextuel 'deuxième graphe', qui se trouve alors coché jusqu'à nouvel ordre.
| Passer à la demi fenêtre de droite (clic-G sur le graphe de droite pour le rendre actif(6)): demander x en ordonnée à gauche, ajouter une 2è courbe en choisissant a à droite |
| NB: l'action de copie de graphe (icône  ou
clic-D sur fenêtre Graphique pour choisir 'copier graphe vers
presse-papier') n'envoie dans le presse-papier que le seul graphe actif
(celui qui est surmonté par le trait horizontal) |
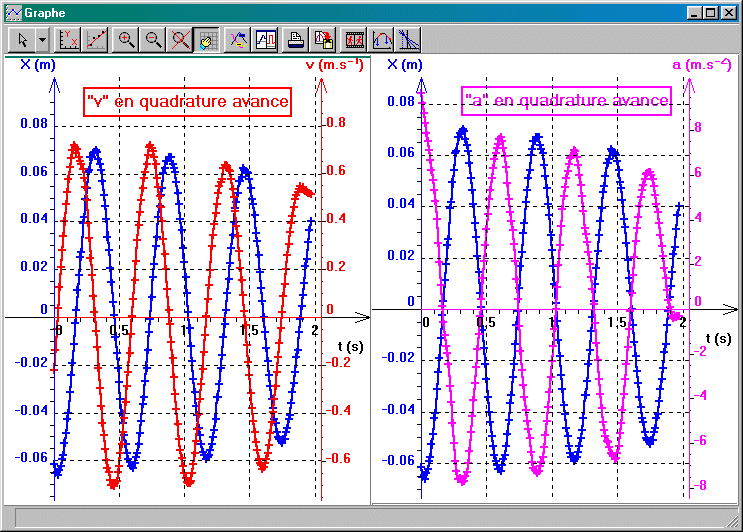
On constate les déphasages: la vitesse est en quadrature avance sur l'abscisse, et l'accélération en opposition de phase.
| Le curseur "Texte" permet de légender chaque graphique; ce qui
nécessite préalablement de "faire de la place" en haut en
diminuant la hauteur des courbes: faire un zoom en forçant manuellement
l'échelle verticale à partir du bouton  ;
dans la boîte de dialogue qui s'ouvre, choisir pour X, v (et a)
un maximum augmenté d'environ 20%. Procéder de même dans le 2è
graphique. |
4. Proportionnalité de x à a: calcul de la pulsation w
On peut vérifier ici la propriété fondamentale de l'oscillateur harmonique donnée par son équation différentielle (a=-
w²*X), par exemple en calculant le rapport a/X. Revenir dans la fenêtre 'Grandeurs'
, onglet 'Expressions', et saisir
directement dans une nouvelle ligne (touche 'Entrée pour revenir à la ligne,
comme dans un traitement de texte) de ce 'mémo':
Coeff = -a/X (7)
pour créer la nouvelle grandeur coeff, et valider par
la touche 'F2' (ou double frappe de la touche 'Entrée') ou en cliquant-G
sur l'icône clignotante 
; la nouvelle variable
apparaît alors dans l'onglet 'Variables'. On arrive à une 1è détermination
|
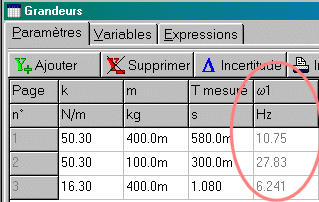
w 1=moy(sqrt(abs(coeff)))Le résultat apparaît dans l'onglet "Paramètres". Ici, on trouve: w1 = 10.8 s-1(unité traduite en Hz par Regressi). Ce résultat peut être confronté aux déterminations ultérieures de w, ainsi qu'à la valeur la période, et à celles de m et k. On trouve ainsi: |
 |
|
|
w 1 |
|
11.2 |
10.8 |
|
22.4 |
27.8 |
|
6.4 |
6.2 |
ce qui représente une incertitude relative d'environ 4% dans les 2 meilleurs cas.
5. Évaluation de la pulsation w par modélisation de w=f(X)
On peut modéliser directement la courbe a(x) par l'équation
a= -w²*X. Pour
cela, fenêtre "Graphiques": cliquer-G sur l'icône ,
et choisir:
 |
|
.Dans la fenêtre 'Graphiques', clic-D pour choisir
'Modélisation' dans le menu contextuel, ou clic-G sur l'icône
correspondante 
(ou touche F9) pour saisir le
modèle:
a= -
w2*w2*Xet cliquer-G sur le bouton "ajuster". On obtient ainsi une nouvelle détermination
w2 du paramètre pulsation w (à comparer à w1): par exemple ici 10,6 au lieu de 10,8.D. Modélisation de x(t) ou R(t); amortissement
Revenir à un seul graphique, représentant par exemple x(t) et v(t). Retirer la 2è courbe (v(t))
| S'assurer préalablement que l'unité d'angles active est
bien le radian: fenêtre "Grandeurs"  ,
onglet "Expressions" (bouton 
visible). |
| Dans la fenêtre 'Graphiques'  ,
clic-D pour choisir 'Modélisation' dans le menu contextuel, ou clic-G sur
l'icône correspondante 
(ou
touche F9): un volet supplémentaire s'ouvre alors dans la partie
gauche de la fenêtre graphique. Saisir dans la zone "Expression du
modèle" le type de fonction choisi sous la forme (ici fonction
sinusoïdale amortie):
|
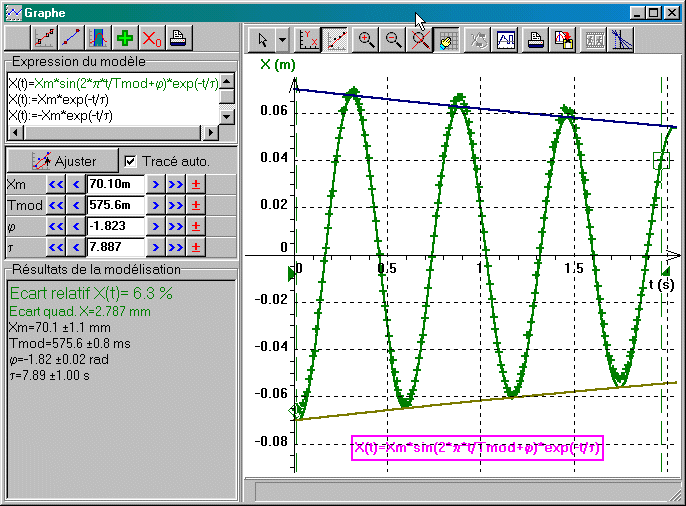
X(t)=Xm*sin(2*p*t/Tmod+f)*exp(-t/t)
et pour tracer automatiquement les enveloppes supérieures et inférieures:
X(t):=Xm*exp(-t/t)
X(t):=-Xm*exp(-t/t)
ce qui demande au logiciel de chercher pour quelles valeurs de Xm, Tmod, f et t la courbe théorique colle au plus près aux points expérimentaux. On peut utiliser en place de saisie manuelle des modèles prédéfinis/ oscillations amorties (accès par clic-G sur icône correspondante(9)
| Demander au logiciel d'ajuster (clic-G sur le bouton
"ajuster"  ) le modèle à la courbe
expérimentale en calculant la valeur des paramètres figurant dans
l'équation du modèle: Regressi passe automatiquement en mode graphique
'points' (au lieu de lissage entre les points), ajuste la courbe modèle aux
points expérimentaux, et ajoute dans l'onglet 'Paramètres' de la fenêtre
'Grandeurs' une colonne par paramètre en y indiquant la valeur calculée
par la modélisation (valeurs des paramètres qui figurent aussi dans la
fenêtre graphique) |
|
 |
On peut aussi placer le curseur dans la case où figure la valeur des autres
paramètres, et en modifier la valeur par clic-G sur les flèches de
défilement 
1/3
situées à côté (NB: changement de signe uniquement par clic sur le
bouton 
), jusqu'à ce que la courbe modèle
s'ajuste aux points expérimentaux (il faut pour cela que le bouton 'Tracé
auto 
soit enfoncé). Cette méthode sera
indispensable si la valeur obtenue pour l'amplitude s'avère négative(10),
et si celle obtenue pour f sort de
l'intervalle {-p , +p
}: les résultats de la modélisation doivent alors être ajustés de façon à
obtenir la détermination principale de j , et
aussi de façon à ce que fréquence et amplitude soient positives (forme
canonique)!
NB: ces valeurs de f ne représentent pas les déphasages des grandeurs entre elles, mais les "phases à l'origine"!
Un clic sur le bouton 
permet de
faire afficher sur le graphique l'équation des modèles (choisir "Options/ Titre
du graphe" dans les versions récentes de Regressi).
Ces déterminations nouvelles de la période fournissent,
moyennant calcul (d'après 
puisqu'on
connaît la masse m, une nouvelle détermination de
la constante de raideur k du ressort:
IV Graphe des paramètres T= f(m) lorsque k est inconnue
Principe de cette étude:
avec un même ressort (donc k constant), on enregistre R(t) avec une
masse m différente dans chaque page d'un même fichier. La modélisation
donne un ensemble de valeurs de T associées aux valeurs de m
(paramètres). Le "graphe des paramètres" est la page(11) qui représente
et permet d'étudier par exemple T en fonction de m, ce qui
permettra par exemple de retrouver; par modélisation dans cette page de la
relation T= f(m), la valeur de k.
A. Acquisition des nouvelles pages avec le MÊME ressort dans un MÊME fichier
1. Acquisitions transférées dans le même fichier
|
 |
(ou
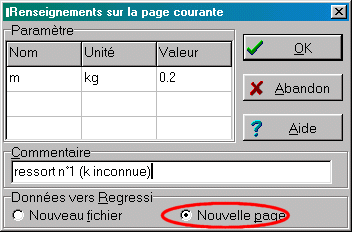par les boutons de la barre des tâches) | Transférer toujours dans une NOUVELLE PAGE du même fichier (en saisissant au passage dans la boite de dialogue du transfert la nouvelle valeur de la masse) |
| Et ainsi de suite, pour constituer autant de pages que de valeurs possibles de m. |
2. Regroupement éventuel dans un fichier UNIQUE d'acquisitions déjà transférées dans plusieurs fichiers
| Ouvrir un des fichiers |
| La commande "Fichier/ Fusionner"(12) permet de choisir le fichier qui sera rajouté dans le fichier ouvert sous forme d'une nouvelle page |
| Procéder ainsi jusqu'à obtenir le nombre de pages souhaitées |
| Sauver le nouveau fichier ainsi obtenu sous un nouveau nom |
NB: les fichiers ainsi réunis doivent obligatoirement avoir la même structure (noms de variables, ordre dans le tableau, etc.)
B. Modélisation de R(t) ou x(t) dans chaque page
Il suffit en faisant défiler les pages successives (clic sur
flèche de défilement 
1/3
sous la barre de menus, ou menu "Pages/Suivante, ou raccourci F8) de
cliquer à chaque fois sur le bouton "Ajuster" 
puisque
le modèle est toujours le même. Les résultats successifs sont stockés au fur
et à mesure dans l'onglet "Paramètres" de la fenêtre
'Grandeurs' 
.
Faire afficher l'équation du modèle avec 
(choisir "Options/ Titre du graphe" dans les versions
récentes de Regressi).
C. Graphe des paramètres T= f(m), et modélisation dans cette nouvelle représentation
| Vérifier dans l'onglet "Paramètres" de la fenêtre "Grandeurs" la présence des colonnes de valeurs en regard pour la période Tmod et la masse m. |
| Ouvrir la fenêtre 'Graphe des paramètres' soit par clic-G sur son icône
 située sous la barre de menus générale (juste à
droite de l'icône 'Statistiques'), soit par le menu 'Fenêtres' |
|
|
de cette fenêtre Graphe des Paramètres, choisir la représentation Tmod= f(m);
constater qu'elle n'est pas linéaire… | Cliquer sur le bouton "Choix des pages" 
de cette page et sélectionner les seules pages se référant à une
même constante de raideur parmi toutes les pages d'acquisition: ce sont
alors les seules pages prises en compte par le logiciel pour les valeurs des
paramètres, càd pour les points (m, Tmod) pris en compte
pour calculer ce nouveau modèle. |
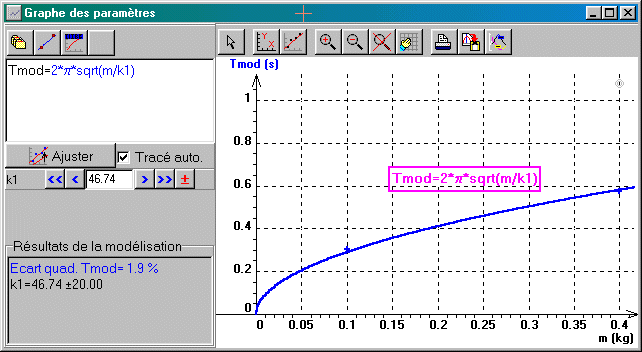
La valeur obtenue pour k concorde avec celle
déterminée par étalonnage. Cliquer sur l'icône 
pour titrer le graphique avec l'équation du modèle.
V Étude énergétique
On suppose ici que les étude précédentes ont permis d'obtenir les valeurs de la vitesse et de l'accélération.
A. Calcul de différentes formes d'énergie
On possède donc tous les éléments pour calculer et
représenter les variations d'énergie mécanique du système. Dans la fenêtre
"Grandeurs", onglet "Expressions", saisir sur une nouvelle
ligne (saut de ligne par touche "Entrée") du "mémo" les
paramètres de page(13), avec leurs unités (sauf si elles figurent déjà
dans l'onglet "Paramètres" de la fenêtre "Grandeurs" 
à la suite des calculs de modélisation):
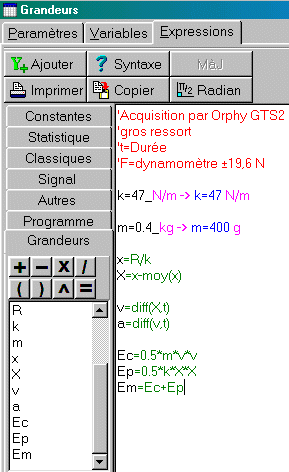
m=0.4_kg
k=47_N/m
Après mise à jour, le logiciel renvoie:
m=0.4_kg -> m=400 g
k=47_N/m -> k=47 N/m
(couleurs au choix dans les "Options générales"). Ces valeurs peuvent donc ensuite être utilisées pour les calculs de nouvelles variables.
1. Énergie cinétique(celle de la masse) Ec= ½ *m*sqr(v) Après validation, la variable correspondante apparaît dans une nouvelle colonne de l'onglet "Variables". 2. Énergie potentielle(celle du ressort) Ep= ½*k*sqr(X) et valider (F2). 3. Énergie mécanique
|
|
B. Visualisation graphique des échanges d'énergie
1. Représentation temporelle
|
Passer dans la Fenêtre "Graphiques" et
demander dans la boîte "Coordonnées", ou |
,
l'affichage en fonction du temps des 3 courbes EpOn peut restreindre éventuellement l'intervalle de temps
affiché (zoom) à partir du bouton 
d'échelle
manuelle: fixer alors la valeur maximum du temps (par exemple 1.0 ms: voir
dernier graphique).
Pour légender les courbes, on peut utiliser:
| soit le bouton automatique d'identification des courbes 
(déplacer ensuite les légendes(14) par cliquer-glisser) |
| Soit le "Curseur texte": cliquer à l'endroit voulu. |
2. Représentation spatiale: puits de potentiel
| Supprimer l'affichage de X à droite, et demander l'affichage en fonction de X des 3 courbes Ep, Ec, et Em à gauche; on observe alors très bien le puits de potentiel de l'oscillateur harmonique, ainsi que le va-et-vient entre les formes cinétique et potentielle de l'énergie. La dissipation progressive d'énergie du système est davantage visible dans le décalage progressif de la courbe Ec(X) |
| on peut se limiter à une seule période, par exemple la première, en
supprimant toutes les lignes suivantes du tableau des variables: sélectionner
toutes les lignes à supprimer en les mettant en sur brillance par un
cliquer-glisser (ou plus rapide: en cliquant à chaque extrémité de
la partie à supprimer et en maintenant enfoncée la touche
"majuscule"), puis appuyer sur  .
|
On peut obtenir la représentation côte à côte des 2 graphiques en utilisant préalablement le bouton
.
Cliquer ici pour ouvrir la documentation complète de Regressi
retour sommaire chapitre en cours
(1) Ce que ne permet pas l'oscillateur harmonique horizontal de Magnum, puisque son mobile et le jeu de ressorts sont uniques.
(2) Du moins si celle de k a été rentrée préalablement… Mais il n'est jamais trop tard…
(3) Du moins si celle de k a été rentrée préalablement… Mais il n'est jamais trop tard…
(4) Les lignes de commentaires sont celles qui débutent par le signe '
(5) Consulter l'aide
sur la syntaxe par l'icône 
(5b) Consulter l'aide
sur la syntaxe par l'icône
(6) Une ligne colorée horizontale marque le haut de la fenêtre de celui des 2 graphes qui est actif.
(7) U (8) dues à l'incertitude logicielle dans le calcul de la dérivée seconde deX (9) Accessible seulement si ce choix a été coché dans l'onglet 'Modélisation' du menu 'Options'. (10) Une solution correcte mathématiquement ne convient pas toujours physiquement! (11) Dans cette page particulière, les variables sont en fait les paramètres des autres pages! (12) Et non pas la commande "Pages/ Grouper" qui a pour effet de réunir dans une seule page les différentes pages d'un même fichier…!(13) Pour les paramètres indépendants des pages, taper quelque chose du type g=9.81 ou m=0.400_g permet d'avoir des formules littérales dans la suite.
(14) modifiables: pour les éditer, double-cliquer sur la légende