I Objectifs
II Montage et mesures
III Saisies et transfert
IV Exploitation des mesures
V Étude complémentaire
I. Objectifs
|
 |
II. Montage et mesures
A. Montage
Dans le dispositif classique, un demi cylindre plein en plexiglas, ou creux et rempli d'eau (ou d'un autre liquide dont on veut déterminer l'indice de réfraction), reçoit un pinceau de lumière blanche provenant d'une lanterne équipée d'une fente. On peut choisir de faire tomber le rayon incident sur face plane (cas traité ici) ou bien sur la face cylindrique (mais dans ce cas, on n'aura pas toujours de rayon émergent pour les grandes incidences). On fait varier ici l'angle d'incidence par la rotation de l'hémicylindre autour de son centre O, la lanterne restant fixe.
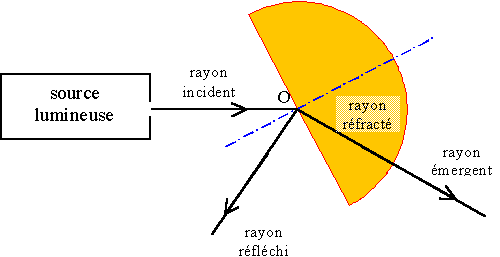
Pour la qualité des mesures, il est important de régler précisément les vis latérales de positionnement de la lanterne de façon que le rayon incident tombe toujours sur le centre O de la face d'entrée.
B. Observations expérimentales
 | On peut noter que, quelle que soit l'incidence, il y a toujours un rayon réfléchi et un rayon émergent (donc aussi un rayon réfracté). On remarque cependant que la proportion d'intensité lumineuse dans le rayon réfléchi augmente avec l'angle d'incidence. |
| Avec l'augmentation de l'angle d'incidence, il apparaît un phénomène (parasite ici puisqu'il gène la mesure de l'angle de réfraction) de décomposition de la lumière dans le rayon émergent: c'est la dispersion de la lumière, due au fait que les différentes longueurs d'onde n'ont pas la même vitesse de propagation dans le milieu transparent. |
| Si on n'a pas encore étudié les lois de la réfraction à ce stade, on admettra qu'il n'y pas de réfraction supplémentaire à travers la face (dioptre) de sortie: rayon émergent et premier rayon réfracté sont alignés. |
C. Mesures
N.B.: les angles sont tous repérés par rapport à la normale au dioptre d'entrée.
Faire varier l'incidence i de façon à obtenir une dizaine ou une quinzaine de mesures entre 0° et 90° (bien inclure ces deux valeurs extrêmes dans les mesures). Quand le pinceau s'élargit, on notera la mesure par rapport au rayon central. A priori, les mesures sont effectuées en degrés d'angle (°).
III. Saisies et transfert
A. Création du fichier de mesures dans Regressi
|
Lancer le logiciel, et choisir dans le menu de gauche: Fichier / Nouveau / Clavier. Renseigner alors la boite de dialogue qui s'ouvre: commentaire général, noms des variables, unité, valeurs extrêmes(1) ; le paramètre pourrait être l'indice n du milieu s'il est connu d'avance. cocher la case "Incrémentation automatique" permettra un remplissage automatique de la valeur de l'angle d'incidence dès que la saisie de ses deux premières valeurs aura fourni au logiciel le pas utilisé. Terminer en validant la boite (touche "Entrée"). Les noms de variables, ainsi que les unités peuvent être modifiés ultérieurement; de la même façon, un commentaire peut être attaché à chaque variable pour préciser sa signification. Pour cela, dans l'onglet "Variables", double cliquer sur la tête de colonne (en grisé) de n'importe laquelle des variables pour faire apparaître la boite de dialogue "Grandeurs" correspondante: saisir un commentaire dans la dernière ligne: ß |
 |
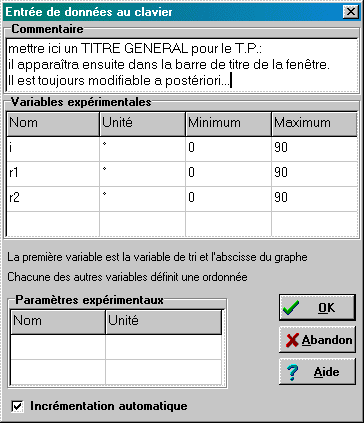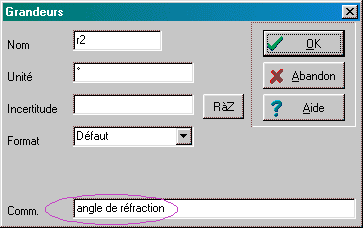
B. Saisie des mesures
Cliquer G sur l'onglet " Variables " de la
fenêtre " Grandeurs ". bien vérifier que l'unité de mesure
courante des angles est le degré: le bouton 
doit être enfoncé de façon à apparaître ainsi 
.
Saisir au clavier les valeurs obtenues pour chaque incidence: la frappe de le
touche 'Entrée" ou de la touche de déplacement de curseur (®
) permet de passer à la cellule suivante.
Disposer la fenêtre "Graphiques"(2) à côté,
de façon à voir se tracer les points expérimentaux au fur et à mesure de
leur saisie. Par défaut, seuls sont affichés les points correspondants à la
première colonne d'ordonnées(3), c'est à dire à la représentation de r2 = f(i)
Pour observer simultanément le graphe r1 = f(i),
cliquer D dans la fenêtre 'Graphiques' pour choisir 'Coordonnées'
dans le menu contextuel, ou cliquer G sur l'icône correspondante 
et
sélectionner:
| i en abscisses |
| r2 en 1è ordonnée (à gauche) |
| r1 en 2è ordonnée (à gauche). |
Lors du passage à la 3è ligne du tableau, la cellule de gauche incrémentera automatiquement le valeur de i si la case correspondante a été cochée dans la boite de dialogue initiale.
Dans un souci de transparence, il est préférable à ce stade de garder la représentation sous forme de points isolés, l'option "lissage"(4) permettant éventuellement de tracer automatiquement la courbe moyenne mais suivant un critère mathématique(5) qui est inconnu des élèves.
C. Édition du graphique
A ce stade plusieurs outils permettent d'améliorer la présentation du graphe:
| Le curseur 'texte' (à choisir dans la liste déroulante) sert à annoter le graphique en y rajoutant une légende avec un cadre ou une flèche: choisir ce curseur (cliquer G sur ce nom dans la liste déroulante des curseurs), cliquer G sur le graphique et maintenir enfoncé le bouton gauche, déplacer la lettre "A" apparue en glissant puis relâchant à l'emplacement choisi pour le commentaire; saisir le commentaire dans l'onglet 'texte' de la boîte qui s'ouvre automatiquement, et choisir entre les différentes présentations possibles dans l'onglet 'options' avant de valider. Ce commentaire peut à tout moment être déplacé par cliquer glisser du pointeur dessus, ou édité par double clic G. |
| Une légende distinguant chaque courbe est ajoutée automatiquement avec
l'icône "Identifier les courbes"  ou
le menu contextuel (clic D /Identifier courbes).
|
IV. Exploitation des mesures
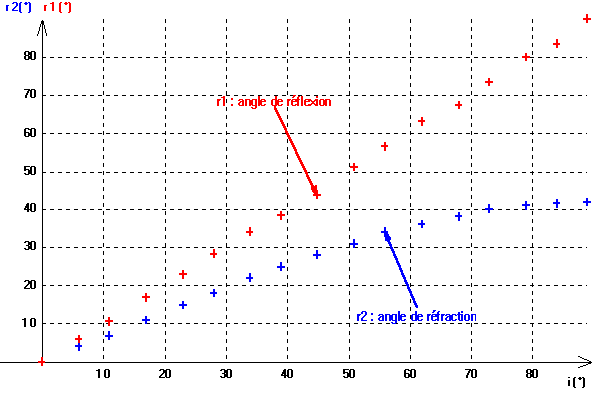
A. Loi de la réflexion r1 = f(i)
Une simple comparaison des colonnes correspondantes du tableau de mesures permet de constater avec une assez bonne précision que:
r1 = i
Le graphique
correspondant r1 = f(i) est donc une demi droite
passant par l'origine. Pour observer sa pente en axes orthonormés, il suffit de
cocher ce choix d'axes dans la boîte 'Coordonnées' (s'ouvre par le menu
contextuel, ou par clic G sur l'icône correspondante 
)
B. Loi de la réfraction r2 = f(i)
Les points sont d'abord assez bien alignés jusque vers 35° d'incidence, puis la courbe s'infléchit nettement vers le bas. Il s'agit de trouver quelle loi mathématique peut relier r2 et i.
1. Principe de la modélisation
|
"Modéliser" cet ensemble de points expérimentaux consiste:
Ce procédé, réalisé automatiquement par Regressi sur demande de l'utilisateur, ayant un coté un peu "magique", il peut être plus pédagogique de réaliser d'abord cette modélisation en tâtonnant manuellement, avant d'utiliser cette fonctionnalité du logiciel. |
 |
2. Essai manuel de différents modèles
On utilise alors Regressi en traceur grapheur de courbes, et on cherche ainsi la courbe d'équation donnée qui se superpose le mieux possible aux points expérimentaux. Passer pour cela dans l'onglet "Expressions" de le fenêtre "Grandeurs", et saisir directement dans une nouvelle ligne:
r'2 = 0.56*i
puis valider (double frappe de la touche "Entrée",
ou touche F2, ou clic sur bouton 
de mise à
jour). En passant alors dans la boite "Coordonnées" de la
fenêtre "Graphiques", la nouvelle fonction r'2 est
disponible dans les listes déroulantes d'ordonnées. Observer le résultat:
avec un coefficient directeur compris entre 0.5 et 0.6 on obtient à peu près
la droite moyenne des points expérimentaux, mais ce modèle linéaire(6) n'est pas
satisfaisant pour les grandes incidences. Il faut peut-être alors suggérer le
modèle sinusoïdal, qu'on peut chercher à optimiser manuellement comme
précédemment (par tâtonnements), ou bien utiliser la fonction de
modélisation (automatique) de Regressi.
3. Modélisation automatique
| Dans la fenêtre 'Graphiques', cliquer-D pour choisir 'Modélisation' dans
le menu contextuel, ou cliquer-G sur l'icône correspondante 
(ou raccourci clavier par touche F9). Saisir dans la zone
"Expression du modèle" le type de fonction choisie sous la forme
(ici fonction linéaire):
|
r2 = a*i
ce qui demande au logiciel de chercher pour quelles valeurs de a la courbe théorique (droite) collera au plus près aux points expérimentaux. On peut utiliser en place de saisie manuelle des modèles prédéfinis (accès par clic-G sur icône(7) correspondante). Puis valider (double frappe de la touche "Entrée", ou touche F2, ou clic sur le bouton
de mise à jour). Les croix qui apparaissent sur les points expérimentaux extrêmes représentent les limites de l'intervalle modélisé: elles peuvent être re positionnées par cliquer glisser du pointeur.
| Demander au logiciel d'ajuster(8) le modèle à la courbe expérimentale
(clic-G sur le bouton "ajuster"  ):
le programme calcule alors la valeur du paramètre a figurant dans
l'équation du modèle, et superpose aux points expérimentaux la courbe
modèle ainsi déterminée. Pour évaluer la pertinence du modèle choisi,
bien regarder l'information affichée par le programme sur l'écart
relatif entre le modèle théorique et les points expérimentaux: ici, ce modèle s'écartant de près de 10%
des points expérimentaux, il n'est pas satisfaisant.
|
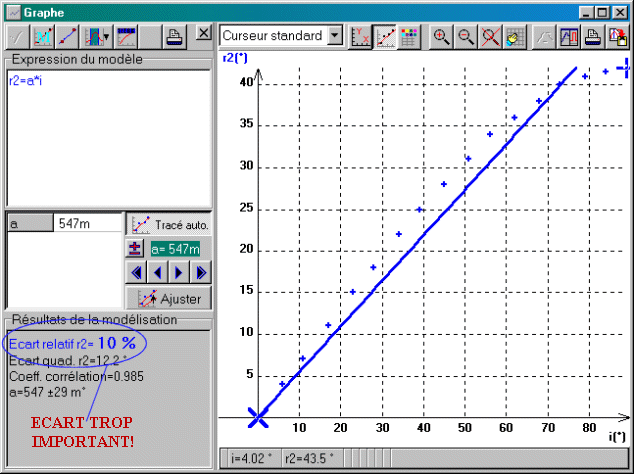
4. Validation de la loi de Descartes. Indice de réfraction
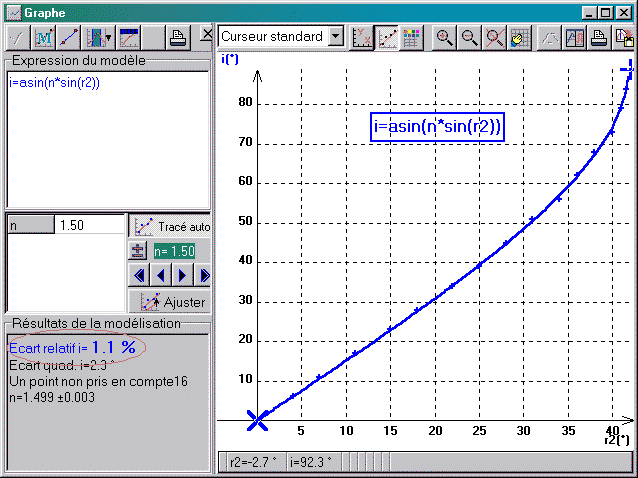
Pour tester le modèle sinusoïdal donné sous forme de fonction implicite par la relation sin(i) = n*sin(r2), il faut saisir à la place du modèle précédent (ou bien à la ligne(9)) l'équation(10):
r2 = asin(1/n*sin(i))
ou bien plus simplement:
i=asin(n*sin(r2))
à condition de permuter entre elles les coordonnées(
); choisir r2 en abscisse, et i en ordonnée. Saisir l'équation du modèle, puis valider comme précédemment et cliquer sur le bouton "Ajuster"
: la valeur de n s'affiche alors. Dans le cas des fonctions trigonométriques, ou quand un paramètre (n ici) se trouve en dénominateur, la recherche automatique peut parfois diverger: il suffit alors d'indiquer dans la case où est affichée la valeur du paramètre une valeur très approximative, et demander à nouveau l'ajustage automatique. S'il y a encore divergence dans ces conditions, il faut faire varier manuellement la valeur(11) du paramètre en plaçant le curseur dans la case où figure cette valeur et en cliquant sur les flèches
d'incrémentation (et décrémentation). En cas de recherche difficile, il peut être utile de désactiver temporairement le bouton. 'tracé auto'
(= position 'sortie').
On obtient directement l'affichage de l'équation du modèle sous forme de titre en cliquant sur le bouton.
On obtient cette fois un écart relatif modèle /expérience de l'ordre de 1%, ce qui valide a posteriori le loi de Descartes, et fournit donc une valeur approchée de l'indice du matériau utilisé, ici n = 1.5 pour le plexiglas.
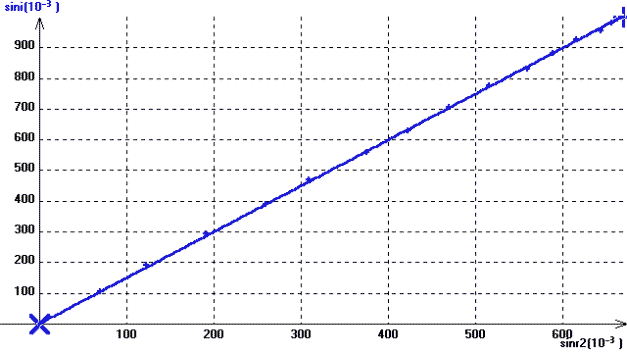
5. Troisième méthode possible: comparaison directe des sinus des angles
Si la fonction "arc sinus" paraît trop complexe à utiliser avec les élèves, une méthode directe privilégiant la découverte sans donner la solution est de calculer dans Regressi sin(i) et sin(r2) puis de comparer entre eux ces deux sinus. Passer dans l'onglet "Expressions" (comme au §IV B 2) pour créer les deux fonctions auxquelles on donnera n'importe quel nom (y et z par exemple) ou mieux sini et sinr2 en saisissant sur deux lignes successives:
sini=sin(i)
sinr2=sin(r2)
puis valider. Passer dan la fenêtre "Graphiques" pour choisir les nouvelles coordonnées: sini en ordonnée, et sinr2 en abscisse. On obtient une demi droite passant par l'origine qu'on peut alors modéliser par:
sini=n*sinr2
pour obtenir la valeur de l'indice en même temps qu'obtenir la loi de Descartes.
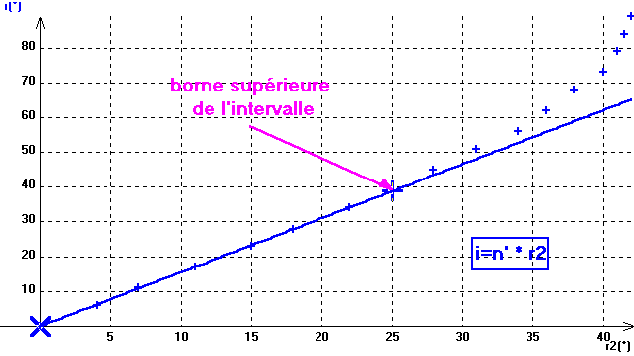
6. Approximation des petits angles: modélisation d'une portion de la courbe
Un modèle peut également s'appliquer à une portion de courbe seulement (c'est à dire dans un certain domaine de validité); on peut suivant le même principe appliquer des modèles différents à des portions différentes (ou communes) d'une courbe expérimentale. On a vu par exemple ici que pour les petits angles les points sont alignés avec l'origine.
Pour pouvoir utiliser la relation sous la forme i = n*r, s'assurer d'abord d'avoir comme coordonnées ( ) r2 en abscisse, et i en ordonnée.
Cliquer G sur , et choisir "Bornes et nouveau modèle": cliquer tirer alors le pointeur ("souris") en maintenant enfoncé le bouton gauche de façon à délimiter la zone choisie (ici la partie rectiligne de la courbe) par la zone grisée rectangulaire qui apparaît, puis relâcher en limite de zone.
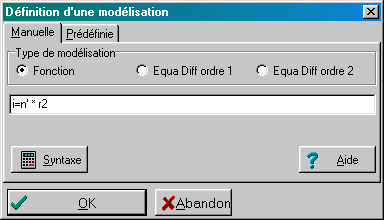
La boîte de dialogue "Définition d'une modélisation" s'ouvre alors automatiquement au relâchement du pointeur; ajouter dans la ligne de saisie l'équation: i(r2)=n' * r2
et valider. On obtient ainsi une nouvelle détermination n' de l'indice en même temps qu'une validation de la loi approximée pour les petits angles.
Les croix indiquant les limites de l'intervalle de modélisation choisi peuvent être déplacées par cliquer tirer du pointeur: un clic sur le bouton "Ajuster" re calcule aussitôt la valeur du paramètre n' pour le nouvel intervalle.
V. Étude complémentaire
L'étude d'un milieu d'indice différent peut être menée ensuite dans une nouvelle page d'acquisition du même fichier de façon à pouvoir comparer directement entre elles les réponses de ces milieux.
|
Pour obtenir ainsi une nouvelle page d'acquisition dans
le même fichier Regressi, choisir 'Page /Nouvelle /Créer page
vierge' dans le menu principal, et remplir le tableau vierge de la
page 2 comme au § III B. Exploiter ensuite comme précédemment. La
navigation entre les différentes pages se fait au moyen des flèches de
défilement |
|
(barre de menus) et en cochant les
seules pages à réunir dans la boite de dialogue qui s'ouvre. La superposition se supprime en revenant aux
mêmes boites (pour décocher).Cliquer ici pour ouvrir la documentation complète de Regressi
retour sommaire chapitre en cours
(1) Indispensables à ce stade, car le logiciel en a besoin pour calculer les échelles nécessaires des axes pur afficher la représentation graphique dès la saisie du premier point.
(2) à
ouvrir par le menu 'Fenêtre /graphe Variables', ou en cliquant
sur l'icône 
.
(3) C'est à dire la deuxième colonne, la première étant considérée par défaut comme une abscisse.
Case à cocher dans la boite "Options": accès par le menu contextuel ouvert par clic D, ou par l'icône
(5) Lissage par une Bspline: plus l´ordre choisi est grand, plus la courbe est proche des points.
(6) Bien qu'étant celui toujours proposé spontanément par les élèves…
(7) Accessible seulement si ce choix a été coché dans l'onglet 'Modélisation' du menu 'Options' (barre principale de menus).
(8) L'ajustement
de la courbe modèle aux points expérimentaux se produit seulement si le bouton
'tracé auto' 
est en position enfoncée.
(9) Une simple frappe de la touche "Entrée" provoque un saut de ligne comme dans un traitement de texte; une double frappe de cette touche provoque la validation du modèle saisi.
(10) L'accès à la syntaxe des fonctions dans Regressi peut se faire
par l'icône 
de la fenêtre
'Grandeurs'.
(11) NB:
changement de signe possible uniquement par clic sur le bouton 
.
(12)
Accès possible aussi en cochant "superposition des pages"
dans la boite d'Options ( 
).