ÉTUDE d'un SIGNAL SINUSOÏDAL
I Objectifs
II Acquisition et transfert
III Modélisation
IV Analyse harmonique
V Définition RMS de la valeur efficace
Ce TP volontairement simple est destiné à une première prise en main de Regressi au travers de ses fonctionnalités de base.
I Objectifs
Étudier les principales propriétés d'une grandeur sinusoïdale:
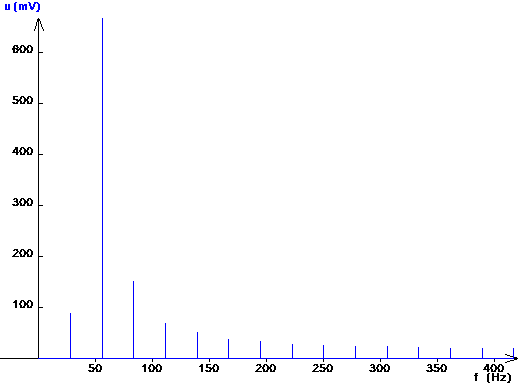
 | Périodicité, et spectre de Fourier; pureté relative du signal (absence ou non d'harmoniques) |
| Accès aux caractéristiques du signal: fréquence, amplitude, valeur moyenne à partir de sa modélisation |
| Définition R.M.S. de la valeur efficace, et comparaison avec la valeur déduite de l'amplitude. |
II Acquisition et transfert
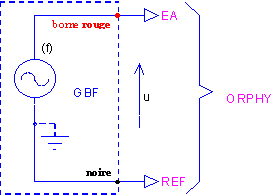
A. Montage et réglage
|
|
|
Deux types de G.B.F. existent:
|
|
NB: Ce problème ne se pose plus en utilisant une entrée différentielle (EAD)!
Abscisse: |
Voies actives: |
Enregistrement: |
Déclenchement (synchro): |
|||||
| Temps t |
EA: |
Variable: |
Signe: |
Cal: |
Unité: |
Nombre points: |
Durée: |
|
|
|
|
|
|
|
|
||
* avec ORPHY-PORTABLE 2, brancher: capsule ±6 V.
Charger l'acquisition pré réglée:
| * avec
ORPHY-GTS 2 |
* avec
ORPHY-GTI 2 |
B. Variables transférées
Ä t et uDans la fenêtre 'Graphiques' (menu Fenêtre/graphe Variables), clic-D
pour choisir 'Coordonnées' dans le menu contextuel, ou clic-G sur l'icône 
:
| t en abscisses |
| u en ordonnées (à gauche) |
On a ainsi la représentation graphique de u=f(t).
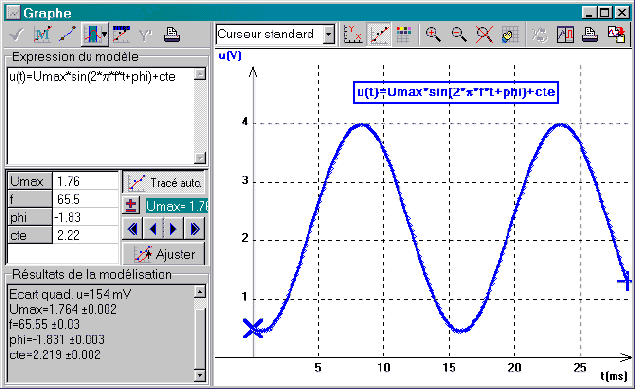
III Modélisation
| Dans la fenêtre 'Graphiques', clic-D pour choisir
'Modélisation' dans le menu contextuel, ou clic-G sur l'icône correspondante |
: un volet supplémentaire s'ouvre alors dans la partie gauche de
la fenêtre graphique. Saisir dans la zone "Expression du modèle" le type de
fonction choisi sous la forme (ici fonction sinusoïdale):u=Umax*sin(2*p *f*t+phi) + Uo
Il est préférable de rajouter le terme "Uo" car beaucoup de GBF délivrent un signal dont la valeur moyenne n'est pas tout à fait nulle; les résultats de la modélisation en seront ainsi améliorés. Pour saisir cette expression où l'unité d'angle est le radian, il faut s'assurer que le bouton
est bien visible et sorti (en position enfoncé, il est remplacé par un symbole en degrés d'angle); sinon, cliquer dessus.
| On peut utiliser en place de saisie manuelle des modèles prédéfinis (accès
par clic-G sur icône  ). Demander au logiciel d'ajuster
(clic-G sur le bouton "ajuster"  ) le modèle à la
courbe expérimentale en calculant la valeur des paramètres figurant dans l'équation du
modèle. | ||
|
| ||
| On obtient ainsi des valeurs expérimentales pour l'amplitude et la fréquence. On peut en déduire la période et la valeur efficace. |
:
l'ajustement de la courbe modèle aux points expérimentaux se produit seulement si le
bouton 'tracé auto' 
IV Analyse harmonique
A. Obtention du spectre
Sous la barre de menus principale, clic-G sur l'icône Fourier
, ou bien choisir 'Fourier' dans le menu
'Fenêtre'; le spectre de Fourier apparaît alors. On peut y choisir le type de fenêtrage
(icônes). Ici, commencer par faire un zoom sur l'intervalle (0; 400 Hz): cliquer-G sur
l'icône 
et cliquer-glisser sur la zone avec le pointeur.
Puis demander dans la liste déroulante le 'curseur données': le déplacement du pointeur
le long du spectre permet de faire ainsi apparaître les coordonnées de chaque raie. Avec
la raie principale, on obtient une nouvelle détermination de la fréquence du signal
étudié. L'importance relative des raies secondaires renseigne sur le caractère non
parfaitement sinusoïdal du signal (l'électronique des GBF génère souvent un signal
sinusoïdal par assemblage de petits segments provenant de morceaux de courbes
exponentielles), c'est à dire sur la présence d'harmoniques.
B. Exportation vers l'imprimante ou un traitement de texte
| On peut copier dans le presse-papiers le tableau des variables (f, u) du spectre
(choix 'copier tableau' dans le menu contextuel ouvert par clic-D sur la fenêtre
'Transformée de Fourier', ou clic-G sur l'icône  ) pour le coller ensuite dans un traitement de texte |
| On peut aussi copier le graphique du spectre (menu général "Édition /
Copier", ou icône  , ou menu contextuel de la
fenêtre 'Transformée de Fourier') |
| On peut imprimer directement le spectre (icône imprimante  ). |
V Définition RMS de la valeur efficace
A .Préliminaire
(rappel: RMS = Root Mean Square, c'est à dire racine carrée de la valeur moyenne du carré du signal étudié)Pour le calcul de l'intégrale correspondante, il faut d'abord se ramener à un intervalle d'une période exacte:
| soit en sélectionnant avant le transfert, si le logiciel d'acquisition le permet, une période seulement |
| soit en supprimant du tableau de valeurs les points superflus: touche
"Majuscule" enfoncée, sélectionner les lignes successives avec le pointeur ou
les touches ¯ , puis cliquer sur l'icône  de suppression |
| soit en supprimant du graphique les points superflus: cliquer-G sur le point, puis appuyer la touche 'Suppr"(3). |
B. Calcul de la fonction valeur efficace
Revenir dans la fenêtre 'Grandeurs', onglet 'Expressions', et saisir directement(4) dans une nouvelle ligne de ce 'mémo':
U=sqrt(moy(sqr(u)))
pour créer la nouvelle grandeur 'valeur efficace' U, et valider
par la touche 'F2' ou en cliquant-G sur l'icône clignotante 
; le
résultat apparaît alors dans l'onglet 'Paramètres'.
C. Comparaison vérification
Il peut être intéressant de visualiser sur le graphique les représentations de u² et de sa moyenne: il suffit pour cela de créer dans une nouvelle ligne du "mémo" les grandeurs fonctions suivantes: | Ucar=sqr(u) |
| Umoycar=moy(Ucar) + 0*t |
| Ueff=sqrt(Umoycar) + 0*t |
N.B. Dans ces derniers cas, le terme 0*t (qui ne change rien sur le plan mathématiques) est une astuce permettant de 'tromper' le logiciel qui a besoin de reconnaître une fonction de t pour la superposer dans le graphique.
Choisir alors dans la fenêtre 'Graphiques' les ordonnées supplémentaires:
| Ucar à droite (car unité différente: V²) |
| Umoycar à droite (idem) |
| Ueff à gauche (en V comme u) |
(Il existe aussi dans Regressi la fonction eff(u) qui donne
directement la valeur efficace)
Comparer alors cette dernière valeur à celle obtenue au par. III à partir de
l'amplitude.
Cliquer ici pour ouvrir la documentation complète de Regressi
retour sommaire chapitre en cours
(2) NB: changement de
signe possible uniquement par clic sur le bouton 
(3) uniquement celle du pavé numérique sous Windows 98! L'accès à la syntaxe des fonctions dans Regressi peut se faire par l'icône "?" de la fenêtre 'Grandeurs'
(4) L'accès à la syntaxe des fonctions dans Regressi peut se faire par l'icône "?" de la fenêtre 'Grandeurs'